[선형대수] Singular Value Decomposition, Pseudoinverse
안녕하세요! 이번 포스트에서는 특이값 분해(Singular Value Decomposition) 와 Pseudoinverse 에 대한 내용을 정리하고자 합니다. 바로 시작하겠습니다 😊
1. 직사각행렬(Rectangular Matrix)에 대하여
앞선 포스트 약 3개 가량이 계속 정방행렬, 특히 대칭행렬에 대한 내용이었다면, 이번 포스트에서 할 내용은 직사각행렬(rectangular matrix), 즉 일반적인 행렬에서 적용할 수 있는 너무나도 중요한 정리에 대한 것입니다! 본격적으로 특이값 분해(SVD)에 들어가기 전에 다음의 예제를 하나 보겠습니다. 참고로, 이 예제는 본문 아래에 참고 교재를 써놓았지만, Linear Algebra and its Applications 7.4 p.433에 수록된 예제입니다.
- 행렬 $\small A=\begin{bmatrix} 4&11&14\cr 8&7&-2\end{bmatrix}$은 아래 그림과 같이, $\small \mathbb{R^n}$의 단위 구 $\small \lbrace \boldsymbol x: \lVert \boldsymbol x\rVert =1\rbrace$를 $\small \mathbb{R^n}$의 타원으로 선형변환시킨다. 이 때, 길이 $\small\lVert A\boldsymbol x\rVert$를 최대화하는 단위벡터 $\boldsymbol x$를 찾고, 이 최대 길이를 구해라.
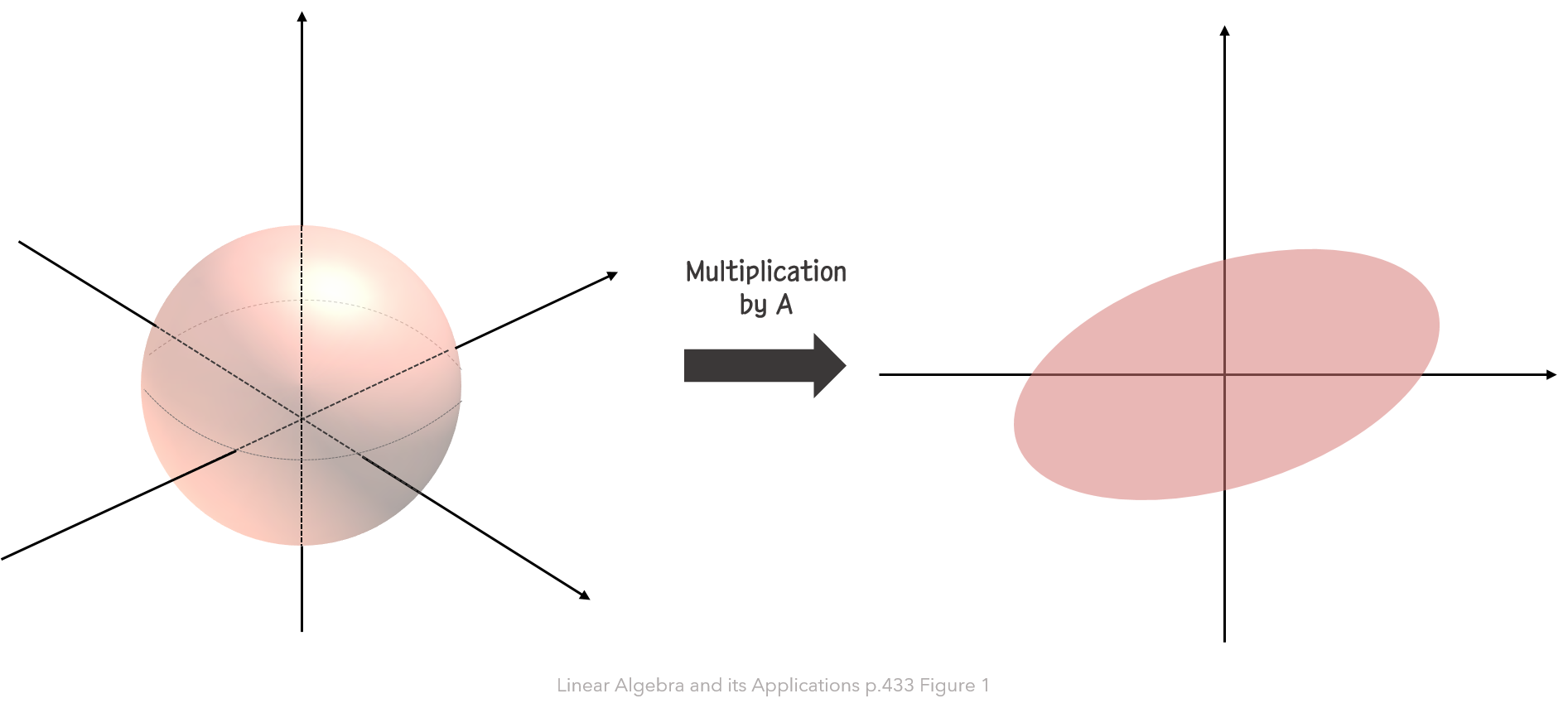
이 문제를 어떻게 해결하면 좋을까요? $\small\lVert A\boldsymbol x\rVert$를 최대화하는 $\boldsymbol x$에서 $\small\lVert A\boldsymbol x\rVert^2$도 최대화할 것입니다. $\small\lVert A\boldsymbol x\rVert^2$를 풀면 다음과 같이 될 것입니다.
\[\lVert A\boldsymbol x\rVert^2=(A\boldsymbol x)^{\intercal}(A\boldsymbol x)=\boldsymbol{x}^{\intercal}A^{\intercal}A\boldsymbol x=\boldsymbol x^{\intercal}(A^{\intercal}A)\boldsymbol x\]즉, $\small\boldsymbol x^{\intercal}(A^{\intercal}A)\boldsymbol x$을 최대화하는 단위벡터 $\boldsymbol x$를 찾으면 되는데, 이 때 $\small A^{\intercal}A$는 대칭행렬입니다! 이거 어디서 많이 보지 않았나요? 바로 저번 포스트에서 단위벡터 하에서 대칭행렬 $A$의 이차형태(quadratic form) $\small \boldsymbol x^{\intercal}A\boldsymbol x$의 최댓값은 $A$의 가장 큰 고유값 $\lambda_1$이라고 했었는데요. 따라서, 제약조건 $\small \lVert \boldsymbol x\rVert=1$ 하에서 $\small\boldsymbol x^{\intercal}(A^{\intercal}A)\boldsymbol x$의 최대값은 $\small A^{\intercal}A$의 가장 큰 고유값 $\lambda_1$입니다. 그런데 이 예제에서는 $\small \lVert A\boldsymbol x\rVert$의 최대값을 구하라고 했기 때문에, 답은 $\sqrt{\lambda_1}$이 될 것입니다. 또 한, 이를 최대화하는 단위벡터 $\boldsymbol x$는 $\small A^{\intercal}A$의 고유값 $\lambda_1$에 해당하는 단위 고유벡터가 됩니다.
2. 특이값(Singular Values)이란?
$A$가 mxn행렬이라고 해봅시다. 그러면 $A^{\intercal}A$는 nxn 대칭행렬이 될 것입니다. 그러면 대칭행렬 포스트에서 했듯이, 대칭행렬 $A^{\intercal}A$는 직교 대각화(orthogonally diagonalizable)가 가능할 것입니다. 이제 $\small\lbrace \boldsymbol{v_1},\boldsymbol{v_2}, \cdots,\boldsymbol{v_n} \rbrace$은 $\small \mathbb{R^n}$의 직정 기저(orthonormal basis)이자 $\small A^{\intercal}A$의 고유벡터라 하고, $\small \lambda_1, \lambda_2, \cdots, \lambda_n$은 각각 이에 해당하는 고유값이라고 하겠습니다. 그러면, $\small i=1,\cdots, n$에 대하여 다음과 같이 나타낼 수 있습니다.
\[\begin{aligned} (A^{\intercal}A)\boldsymbol{v_i} &=\lambda_i\boldsymbol{v_i} \cr \boldsymbol{v_i^{\intercal}}(A^{\intercal}A)\boldsymbol{v_i} &=\boldsymbol{v_i^{\intercal}}\lambda_i\boldsymbol{v_i} \cr (A\boldsymbol{v_i})^{\intercal}(A\boldsymbol{v_i}) &=\lambda_i \boldsymbol{v_i^{\intercal}}\boldsymbol{v_i}\cr \implies \lVert A\boldsymbol{v_i}\rVert ^2&=\lambda_i\lVert \boldsymbol{v_i}\rVert^2=\lambda_i\ge0\end{aligned}\]위 식에 의하여, $\small A^{\intercal}A$의 모든 고유값들은 항상 0이상이라는 것을 알 수 있습니다. 따라서, 이 고유값들에 루트를 씌울 수 있게 되고, 다음과 같이 고유값들에 루트를 씌운 것($\sigma_i$)을 바로 $A$의 특이값(singular value) 이라고 합니다.
\[\sigma_i=\sqrt{\lambda_i},\quad for\space 1\le i\le n\]즉, $A$의 특이값 $\sigma_i$는 벡터 $\small A\boldsymbol{v_i}$의 길이를 의미하게 됩니다.
특이값들은 항상 0이라는 것을 알았습니다. 이제 n개의 특이값을 그 값이 큰 순서대로 나열해봅시다. 그러면 어떤 $\small 0\le r\le n$에 대하여, $\sigma_r$ 이후부터는 0이 될 수도 있을 것입니다. 0이 고유값이 되는 경우도 많죠? 특이값이 0이 되는 부분과 아닌 부분을 일반화해서 정의하고자 임의의 상수 $r$부터는 0이라고 해보겠습니다.
\[\sigma_1\ge\sigma_2\ge\cdots\sigma_r >0=\sigma_{r+1}=\cdots =\sigma_n\]이 경우를 다시 표현하면, $\small \lVert A\boldsymbol{v_{r+1}}\rVert=\cdots =\lVert A\boldsymbol{v_n}\rVert=0$이 된다는 것이고, 즉 $\small A\boldsymbol{v_{r+1}}=\cdots=A\boldsymbol{v_n}=0 $이 된다는 것입니다. 이제 그렇다면, $r$개의 0이 아닌 특이값들에 대해, $\small A\boldsymbol{v_1},\cdots,A\boldsymbol{v_r}$도 0이 아닐 텐데요. 이들은 어떤 역할을 할까요? 이와 관련하여 아래의 정리를 봅시다.
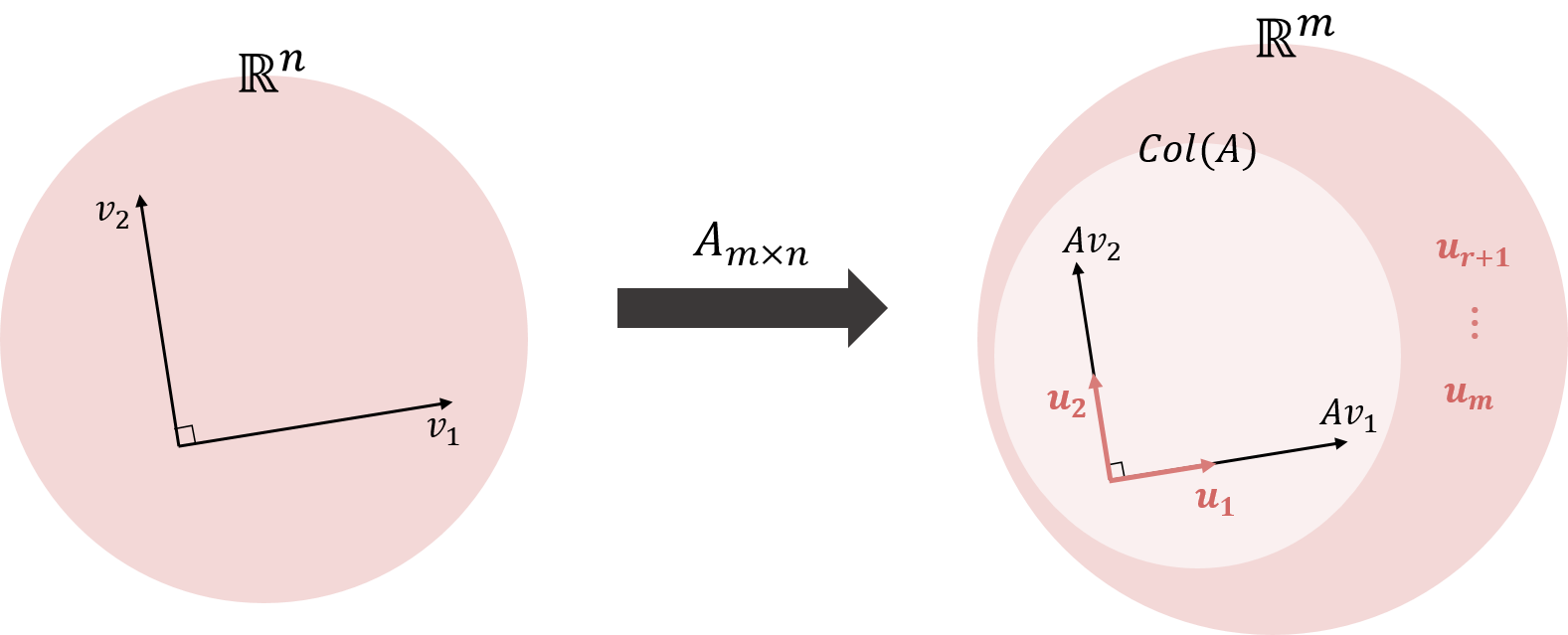
Thm. $\small A^{\intercal}A$의 고유벡터로 이루어진 $\small \lbrace \boldsymbol{v_1},\cdots,\boldsymbol{v_n}\rbrace$이 $\small \mathbb{R^n}$의 직정 기저(orthonormal basis)라고 하고, $A$가 r개의 0이 아닌 특이값들을 가지고 있다고 하자. 그러면, $\small \lbrace A\boldsymbol{v_1},\cdots, A\boldsymbol{v_n} \rbrace$이 $\small Col(A)$의 직교 기저(orthogonal basis)가 될 것이며, $\small rank(A)=r$이 될 것이다.
간단히 증명해 봅시다. 먼저 $i\not =j$일 때, $\small \boldsymbol{v_i}$와 $\small \lambda_j\boldsymbol{v_j}$는 서로 직교하기 때문에, 다음과 같이 $A\boldsymbol{v_i}$와 $A\boldsymbol{v_j}$는 서로 직교하는 것을 확인할 수 있습니다.
\[(A\boldsymbol{v_i})^{\intercal}(A\boldsymbol{v_j})=\boldsymbol{v_i}^{\intercal}A^{\intercal}A\boldsymbol{v_j}=\boldsymbol{v_i}^{\intercal}(\lambda_j\boldsymbol{v_j})=0\]따라서 $\small \lbrace A\boldsymbol{v_1},\cdots,A\boldsymbol{v_n}\rbrace$는 직교 집합입니다. 이제 이 집합이 $\small Col(A)$의 기저라는 것을 보여야 하는데요. 어떤 임의의 벡터 $\small \boldsymbol{x}\in\mathbb{R^n}$에 대해, $\small\boldsymbol y=A\boldsymbol x$라고 한다면, 벡터 $\small\boldsymbol y\in Col(A)$가 될 것입니다. 한편, 벡터 $\boldsymbol x$는 $\small\boldsymbol x=c_1\boldsymbol{v_1}+\cdots+c_n\boldsymbol{v_n}$과 같이 나타낼 수 있을 것 같습니다. 이 때, r개의 특이값들이 0이 아니라고 했으므로, $\small 1\le i\le r$에 대해서는 $\small A\boldsymbol{v_i}\not= 0$이 될 것입니다.
\[\begin{aligned} \boldsymbol y&=A\boldsymbol x =c_1A\boldsymbol{v_1}+\cdots+c_rA\boldsymbol{v_r}+c_{r+1}A \boldsymbol{v_{r+1}}+\cdots+c_nA\boldsymbol{v_n}\cr &=c_1A\boldsymbol{v_1}+\cdots+c_rA\boldsymbol{v_r}+0+\cdots+0\end{aligned}\]따라서 $\boldsymbol y \in\small Span\lbrace A\boldsymbol{v_1},\cdots, A\boldsymbol{v_r}\rbrace$가 되고, $\small \lbrace A\boldsymbol{v_1},\cdots, A\boldsymbol{v_r}\rbrace$은 $\small Col(A)$의 직교 기저가 됩니다. 또 한, $\small rank(A)=din(Col(A))=r$이 됩니다.
3. 특이값 분해(Singular Value Decomposition)
본격적으로 특이값 분해에 대해 알아보겠습니다. 먼저 정리부터 읽어봅시다.
Thm. The Singular Value Decomposition $A$가 rank가 r인 mxn 행렬이라고 하자. 그러면, mxm 직교 행렬(orthogonal matrix) $U$와 nxn 직교행렬 $V$, 그리고 mxn행렬 $\Sigma$가 존재하여 행렬 $A$가 다음과 같이 분해된다: $A=U\Sigma V^{\intercal}$
이 때, 행렬 $\Sigma$는 다음과 같이 대각요소가 $A$의 r개의 특이값들인 대각행렬 $D$와 나머지는 0인 요소들로 이루어진다. \(\small\Sigma=\begin{bmatrix} D &0\cr 0&0\end{bmatrix},\space D=\begin{bmatrix} \sigma_1&&0\cr &\ddots&\cr 0 & &\sigma_r\end{bmatrix}\)
$\small A=U\Sigma V^{\intercal}$와 같이 분해하는 것을 행렬 $A$의 특이값 분해(SVD)라고 하는데요. 이 때, 행렬 $U$와 $V$는 유일한(unique) 것은 아니지만, $\Sigma$의 대각요소 중 첫 r개는 $A$의 특이값으로 유일하게 정해집니다.
이제 이 정리를 증명해봅시다. 2번에서 했던 정리와 증명을 조금 갖다 쓸 건데요. 2번에서 했던 정리에서 가정한 것과 같이, $\small \lbrace \boldsymbol{v_1},\cdots,\boldsymbol{v_n}\rbrace$이 $\small\mathbb{R^n}$의 직정 기저라고 하겠습니다. 그 정리에 의해, $\small\lbrace A\boldsymbol{v_1},\cdots,A\boldsymbol{v_r}\rbrace$는 $\small Col(A)$의 직교 기저입니다. 이제 이 벡터들을 각각의 길이로 나누어서 직정 기저 $\small\lbrace \boldsymbol{u_1},\cdots,\boldsymbol{u_r}\rbrace$를 구하면 다음과 같습니다.
\[\begin{gathered}\boldsymbol{u_i}=\frac{1}{\lVert A\boldsymbol{v_i}\rVert}A\boldsymbol{v_i}=\frac{1}{\sigma_i}A \boldsymbol{v_i} \cr \implies A\boldsymbol{v_i}=\sigma_i\boldsymbol{u_i},\space (1\le i\le r) \end{gathered}\]이제 $\small \lbrace \boldsymbol{u_1},\cdots,\boldsymbol{u_r}\rbrace$을 확장하여 $\mathbb{R^m}$의 직정 기저 $\small \lbrace \boldsymbol{u_1},\cdots,\boldsymbol{u_m}\rbrace$을 얻고, 다음과 같이 이 벡터들을 행렬로 표현하여 이들을 각각 $U$와 $V$라고 하겠습니다.
\[U=\begin{bmatrix} \boldsymbol u_1&\cdots&\boldsymbol u_m\end{bmatrix},\quad V=\begin{bmatrix}\boldsymbol v_1&\cdots&\boldsymbol v_n\end{bmatrix}\]이 때, 두 행렬의 곱 $\small AV$는 다음과 같이 표현할 수 있을 것입니다.
\[\begin{aligned} AV&=\begin{bmatrix} A\boldsymbol v_1 &\cdots&A\boldsymbol v_r &A\boldsymbol v_{r+1}&\cdots&A\boldsymbol v_n \end{bmatrix}\cr &=\begin{bmatrix} A\boldsymbol v_1 &\cdots&A\boldsymbol v_r &\boldsymbol 0&\cdots&\boldsymbol 0 \end{bmatrix}\cr &=\begin{bmatrix} \sigma_1\boldsymbol u_1 &\cdots& \sigma_r \boldsymbol u_r &\boldsymbol 0&\cdots&\boldsymbol 0 \end{bmatrix} \end{aligned}\]한편 $\small U\Sigma$는 어떻게 될까요?
\[\begin{aligned} U\Sigma&=\begin{bmatrix} \boldsymbol u_1 &\cdots & \boldsymbol u_m \end{bmatrix}\begin{bmatrix} \begin{array}{ccc|c}\sigma_1&&0&\cr &\ddots&&\boldsymbol 0\cr 0 &&\sigma_r&\cr \hline & \boldsymbol 0 & &\boldsymbol 0\end{array}\end{bmatrix}\cr &=\begin{bmatrix} \sigma_1\boldsymbol u_1 &\cdots& \sigma_r \boldsymbol u_r &\boldsymbol 0&\cdots&\boldsymbol 0 \end{bmatrix}\cr &=AV\end{aligned}\]따라서 행렬 $V$는 직교행렬이므로, $A$는 다음과 같이 분해가 됩니다.
\[AV=U\Sigma \implies A=U\Sigma V^{\intercal}\]
이해가 되셨나요? 행렬 $V$와 $U$에 대해 더 알아봅시다. 일단 행렬 $A$를 transpose하면 다음과 같이 될 것입니다.
이제, $\small A^{\intercal}A$을 계산해보면 다음과 같이 될 것입니다. 이 때, $\small \Sigma^{\intercal}\Sigma$은 첫 대각요소가 r개의 $\small \lambda_i=\sigma_i^2$이고 나머지는 모두 0으로 이루어진 nxn 대각행렬이 될 것이고, 이를 $D$라고 하겠습니다.
\[\begin{aligned}A^{\intercal}A&=V\Sigma^{\intercal} U^{\intercal}U\Sigma V^{\intercal}=V\Sigma^{\intercal}\Sigma V^{\intercal}\cr &=V\begin{bmatrix} \begin{array}{ccc|c}\lambda_1&&0&\cr &\ddots&&\boldsymbol 0_{\sf (n-r)xr}\cr 0 &&\lambda_r&\cr \hline & \boldsymbol 0_{\sf r x (n-r)} & &\boldsymbol 0\end{array}\end{bmatrix}V^{\intercal}=VDV^{\intercal}\cr &\implies (A^{\intercal}A)V=VD\end{aligned}\]즉, 위에서 최종적으로 도출되는 식에 의해 행렬 $V$는 $\small A^{\intercal}A$의 고유벡터 행렬이라는 것을 알 수 있습니다. 반대로 $\small AA^{\intercal}$을 구하면 다음과 같이 될 것이고, 이번엔 $\small \Sigma\Sigma^{\intercal}$이 첫 대각요소가 r개의 $\small \lambda_i=\sigma_i^2$이고 나머지는 모두 0으로 이루어진 mxm 대각행렬 $D’$가 될 것입니다.
\[\begin{aligned}AA^{\intercal}&=U\Sigma V^{\intercal}V\Sigma^{\intercal} U^{\intercal}=U\Sigma\Sigma^{\intercal}U^{\intercal}=UD'U^{\intercal}\cr &\implies (AA^{\intercal})U=UD' \end{aligned}\]따라서, 위 식에 의해 행렬 $U$는 $AA^{\intercal}$의 고유벡터 행렬이라는 것을 알 수 있습니다!
4. Reduced SVD와 Pseudoinverse
지금까지 SVD에 대해 알아보았는데요. 계산 문제를 조금 풀어보면 아시겠지만, mxn행렬 $A$에 대하여 특이값이 0인 것이 존재하게 되면, 다른 말로 $\small rank(A)<min(m,n)$인 경우에는 계산 과정에서 0이 되는 부분이 매우 많습니다. 따라서, 처음부터 이 0이 되는 부분을 제거하고 계산하면 조금은 더 간단해질 수 있겠죠? 이제 $\small r=Rank(A)$라고 합시다. 그러면, 행렬 $U$와 $V$는 다음과 같이 두 블럭으로 쪼갤 수 있을 것입니다.
\[\begin{aligned} U&=\begin{bmatrix} U_r&U_{m-r} \end{bmatrix}, \quad U_r=\begin{bmatrix} \boldsymbol u_1 & \cdots \boldsymbol u_r\end{bmatrix}\cr V&=\begin{bmatrix} V_r&V_{n-r} \end{bmatrix}, \quad V_r=\begin{bmatrix} \boldsymbol v_1 & \cdots \boldsymbol v_r\end{bmatrix} \end{aligned}\]이 때, SVD 정리를 적용하면 다음과 같이 $\small U_rDV_r^{\intercal}$만 남을 것입니다.
\[A=\begin{bmatrix} U_r&U_{m-r} \end{bmatrix}\begin{bmatrix} D_{\sf rxr}&0\cr0&0\end{bmatrix}\begin{bmatrix} V_r^{\intercal}\cr V_{n-r}^{\intercal}\end{bmatrix}=U_rDV_r^{\intercal}\]이렇게 $A$를 분해하는 것을 $A$의 Reduced Singular Value Decomposition 이라고 부릅니다. 이렇게 분해하면 엄청난 장점이 생기는데요. 바로 행렬 A의 역행렬을 구할 수 있다는 것입니다. 다음의 행렬 $\small A^{+}$을 바로 pseudoinverse 라고 부릅니다!
이렇게 행렬 $A$의 역행렬을 구할 수 있게 되면 많은 것을 할 수 있게 되는데요. 그 중에서도 $\small A\boldsymbol x=\boldsymbol b$와 같은 방정식에 대한 해도 쉽게 구할 수 있다는 것입니다. 이것에 대한 내용은 최소제곱해에 대한 포스트에서 많이 다뤘는데요. SVD를 이용하게 되면, 특별한 조건이 없는 직사각행렬에 대해서도 최소제곱해를 쉽게 구할 수 있게 됩니다.
\[\boldsymbol{\hat x}=A^+\boldsymbol b=V_rD^{-1}U_r^{\intercal}\boldsymbol b\]여기까지 굉장히 활용도가 높은 특이값 분해에 대한 내용이었습니다! 감사합니다 :)
$Reference.$
- David C.Lay · Stephen R.Lay · Judi J.McDonald, Linear Algebra and its Applications, 5th edition, Pearson
- 고려대학교 김홍중 교수님의 수업