[선형대수] Diagonalization
안녕하세요! 이번 글에서는 대각화(Diagonalization) 의 개념 및 정리(theorem)를 살펴보고자 합니다. 바로 시작하겠습니다 :)
1. 대각화(Diagonalization)의 정의
먼저 대각화의 정의부터 알아볼까요?
Def. 어떤 정방행렬 $A$가 $A=PDP^{-1}$, $\small ( P:invertible,D:diagonal)$ 로 나타낼 수 있다면, A는 대각화가 가능하다(diagonalizable).
어떤 정방행렬$(square\space matrix)$ A가 위와 같이 역행렬이 존재하는 어떤 행렬과 대각행렬의 곱으로 쪼개질 때, 다시 말해서 대각행렬 D와 유사(similar)할 때, A는 대각화가 가능하다 고 말합니다. 왜 굳이 이렇게 쪼갤까요? 대각행렬로 표현하면 연산 과정이 간단해지고 해석이 용이하다는 등 장점이 많아지기 때문입니다! 예를 들어, A가 대각화가 가능하다고 해봅시다.
위와 같이 계속 진행하여 일반화하면 결국 $\small A^k=PD^k P^{-1},k≥1$와 같이 나타낼 수 있습니다. 이 때, 대각행렬 $D$의 k번 거듭제곱은 대각 요소들에 각각 k번 거듭제곱만 하면 되기 때문에 계산이 확실히 간단해집니다.
일단 여기까지 대각화가 무엇인지와 대각화를 하는 이유에 대해서 알았습니다. 그러면 이제 정방행렬을 어떻게 대각화하는지 알아야 합니다. 그 전에, 모든 정방행렬을 대각화할 수 있는 걸까요? 확인해봅시다.
2. 언제 대각화가 가능할까?
주어진 정방행렬이 대각화가 가능한지 아닌지 어떻게 알고, 가능하다면 어떻게 대각화할 수 있을까요? 이와 관련하여 중요한 정리는 다음과 같습니다.
Diagonalization Theorem: nxn 행렬 A가 대각화가 가능하기 위한 필요충분조건은 A가 n개의 선형독립인 고유벡터를 가지고 있는 것이다. 다른 말로, $A=PDP^{-1}$이기 위한 필요충분조건은, $invertible\space matrix\space P$의 열들이 서로 선형독립인 A의 고유벡터이고, 대각행렬 $D$의 대각요소들은 $P$의 열들에 해당하는 A의 고유값들인 것이다.
즉, 위 정리에 의해 정방행렬의 대각화는 고유값과 고유벡터를 이용해서 이루어집니다! 왜 그런지 찬찬히 이해해봅시다. nxn 행렬 A가 서로 선형독립인 n개의 고유벡터를 가지고 있다고 합시다.
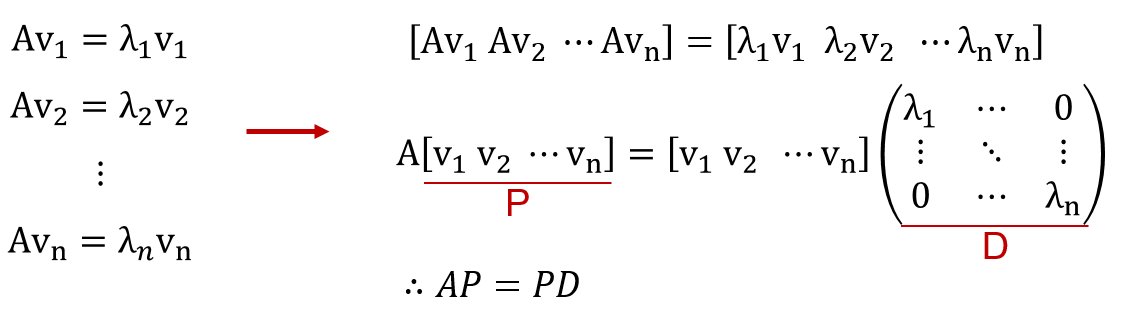
위 그림과 같이 행렬 A의 고유값과 고유벡터를 모두 구하면, 결국 $AP=PD$의 형태로 나타낼 수 있고, 이 때 $P$는 역행렬이 존재하기 때문에 $A=PDP^{-1}$, 즉 $A$를 대각화할 수 있게 됩니다. 그렇다면, 위 정리를 통해 유추할 수 있는 정리가 있게 되는데요. 이는 다음과 같습니다.
Thm. 어떤 nxn 행렬이 n개의 서로 다른 고유값이 존재한다면, 이 행렬은 대각화가 가능하다.
서로 다른 고유값에 대해 그에 해당하는 각각의 고유벡터는 서로 선형독립이다는 정리를 저번 포스트에서 언급했었는데요:) 이 정리에 따라, n개의 선형독립인 고유벡터들이 존재하게 되므로 당연히 대각화가 가능합니다!
그러면 이제 여기서 의문점이 하나 생깁니다. 어떤 행렬의 고유값이 두 개 이상 같은 것이 존재한다면 그 행렬은 대각화가 불가능한 것일까요? 항상 그렇지는 않습니다!
nxn행렬 A가 서로 다른 고유값 $λ_1, λ_2,⋯,λ_p,(p≤n)$ 을 가지고 있고, 각 고유값은 각각 $\small n_1,n_2,⋯,n_p,(n_1+n_2+⋯+n_p=n)$개씩 존재한다고 해봅시다. 그리고 각 고유값에 해당하는 서로 독립인 고유벡터들, 즉 각 고유공간의 차원이 각각 $\small m_1,m_2,⋯,m_p$라고 하겠습니다.
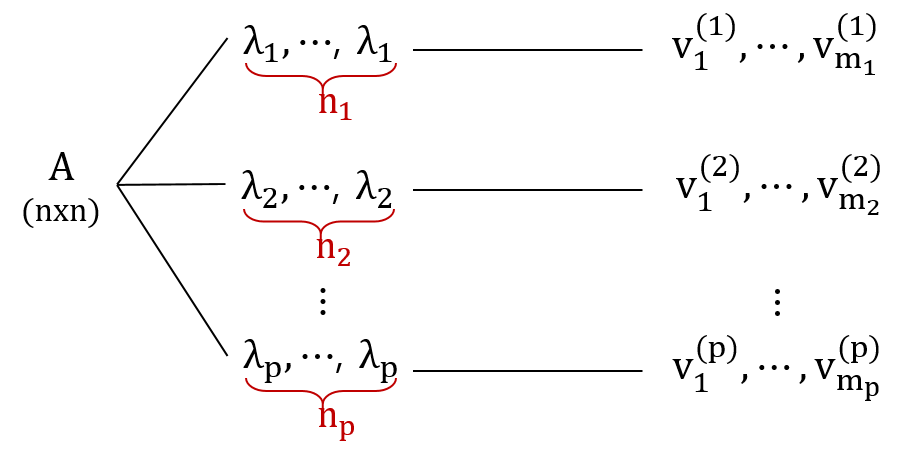
이와 관련한 정리는 다음과 같습니다.
a. (일반적으로) 고유값 $λ_k$, $\small (1≤k≤p)$ 의 고유공간의 차원 $\small m_k$는 $λ_k$의 개수보다 작거나 같다. $\small (1≤m_k≤n_k)$
b. 행렬 A가 대각화가 가능하기위한 필요충분조건은 각 고유값의 개수와 고유공간의 차원이 같아지는 것이다. $\small (m_k=n_k \Rightarrow m_1+m_2+⋯m_p=n)$
위 정리에 의하면, 어떤 고유값이 r개 존재할 때, 그 고유값의 고유공간의 차원이 r이면 대각화가 가능하다는 것입니다! 예를 들어, 3x3 행렬의 고유값이 1,2,2라고 할 때, 고유값 1의 고유공간의 차원은 1이고, 고유값 2의 고유공간의 차원이 2가 된다면 A는 대각화가 가능하게 되는 것입니다! 서로 독립인 고유벡터들이 3개 나왔으니까 $P$의 열들은 모두 선형독립이고 $P$는 역행렬이 존재할 수 있게 되기 때문이겠죠.
지금까지 대각화의 전반적인 개념에 대해서 알아보았습니다! 마지막으로 대각화를 적용할 수 있는 예제를 하나 살펴보고 포스팅을 마무리하고자 합니다. 피보나치 수열 잘 아시죠?
${a_n }: 1\space 1\space 2\space 3\space 5\space 8\space \cdots $ 에서, $a_{502}$은 어떻게 구하면 될까요? 행렬의 대각화를 이용하면 굉장히 쉽게 풀립니다! 피보나치 수열은 아래 두 식으로 표현이 가능한데요.
이를 행렬로 표현하면 다음과 같이 A라는 행렬을 얻을 수 있게 됩니다.
\[\begin{pmatrix}a_{n+2}\\a_{n+1}\end{pmatrix}= \begin{pmatrix}1&1\\1&0\end{pmatrix} \begin{pmatrix}a_{n+1}\\a_{n}\end{pmatrix}\iff x_{n+1}=Ax_n\]이 때, 다음과 같이, $a_{n+2}$와 $a_{n+1}$은 A의 n차 거듭제곱 꼴을 구하면 구할 수 있게 됩니다!
\[\begin{pmatrix}a_{n+2}\\a_{n+1}\end{pmatrix}=x_{n+1}=Ax_n=A^2x_{n-1}=\cdots=A^nx_1=A^n\begin{pmatrix}1\\1\end{pmatrix}\]이제 $\small A^{500}$만 구하면 $a_{502}$도 구할 수 있게 됩니다. $\small A^{500}$을 쉽게 구하기 위해, A의 고유값과 고유벡터를 구해서 대각화 꼴로 만들어줍니다. 고유벡터 구하는 과정은 생략하였습니다.
\[\begin{aligned} |A-\lambda I|&=\begin{vmatrix}1-\lambda&1\\1&-\lambda\end{vmatrix}=\lambda^2-\lambda-1=0\\ &\implies \lambda_1,\lambda_2=\frac {1\pm\sqrt 5}{2} \end{aligned}\]따라서, A는 다음과 같이 대각화 꼴로 만들어질 수 있고, 이를 이용하여 $a_{502}$를 구할 수 있게 됩니다.
\[A=P\begin{pmatrix}\lambda_1&0\\0&\lambda_2\end{pmatrix} P^{-1}\implies A^{500}=P \begin{pmatrix}\lambda_1^{500}&0\\0&\lambda_2^{500}\end{pmatrix} P^{-1}\]이해가 좀 되셨나요? 여기까지는 벡터들이 서로 선형독립이라는 조건만을 가지고 내용을 다뤘는데, 이제 본격적으로 벡터들이 직교한다는 개념을 배우고 그에 관한 다양한 성질과 정리를 다루고자 합니다. 다음 글에서는 직교성(Orthogonal property)에 대해 포스팅하겠습니다. 감사합니다!
$Reference.$
- David C.Lay · Stephen R.Lay · Judi J.McDonald, Linear Algebra and its Applications, 5th edition, Pearson
- 고려대학교 김홍중 교수님의 수업