[선형대수] Eigenvalue, Eigenvector, Character Equation

---

안녕하세요 여러분! 이번 글에서는 고유벡터(Eigenvector) 와 고유값(Eigenvalue), 그리고 특성방정식(Characteristic Equation) 의 개념에 대해서 정리하고자 합니다. 고유값과 고유벡터는 앞으로 포스트할 내용들의 베이스이기 때문에 간단하게 한번 짚고 넘어가겠습니다!

1. 고유값(Eigenvalue)과 고유벡터(Eigenvector)

먼저 고유값과 고유벡터입니다. 정의부터 알아볼까요?

• 정방행렬 $A$의 고유벡터(Eigenvector)란, 어떠한 $scalar\space \lambda$에 대하여 식 $A\boldsymbol{x}=\lambda\boldsymbol{x}$을 만족하는 0이 아닌 벡터 ${\boldsymbol x}$을 의미한다.
• 정방행렬 $A$에 대하여 식 $A\boldsymbol{x}=\lambda\boldsymbol{x}$이 $nontrivial\space solution$ 을 가질 때, 이 때의 $scalar\space \lambda$를 고유값(Eigenvalue)이라 하고, $\boldsymbol{x}$를 $\lambda$에 해당하는 고유벡터라 한다.

결국 식 $A\boldsymbol{x}=\lambda\boldsymbol{x}$을 만족하는 $\lambda$와 $\boldsymbol{x}$가 각각 고유값, 고유벡터라는 것이 내용의 전부입니다. 물론, $\boldsymbol{x}$가 nontrivial solution일 때만 해당합니다! 당연히 $\boldsymbol{x}$가 0이면 항상 위 식은 자명하게 성립하겠죠? 따라서 $\boldsymbol{x}$가 0인 경우를 제외하고도 위 식이 풀릴 때, 그 때의 $\lambda$, $\boldsymbol{x}$ 가 우리의 관심사입니다.

그렇다면 $A\boldsymbol{x}=\lambda\boldsymbol{x}$ 이 식이 의미하는 게 무엇일까요? $A$는 행렬(nxn)이고$\lambda$는 스칼라(1x1)입니다. 이 식의 좌변$(A\boldsymbol{x})$은 어떠한 벡터(nx1) $\boldsymbol{x}$가 행렬 $A$에 의해 선형변환(linear transformation) 된 벡터를 의미하고, 우변$(\lambda \boldsymbol{x})$은 똑같은 벡터 $\boldsymbol{x}$에 어떠한 상수$\lambda$를 곱함으로써 이것의 크기(scale)가 변화된 벡터를 의미할 것입니다. 이 둘이 같다는 것은 결국,어떠한 벡터를 선형변환시켜도 이것의 크기만 변하고 방향은 유지된다는 것을 의미합니다!

자, 그럼 실제로 nxn행렬인 $A$에 대하여, $A\boldsymbol{x}=\lambda\boldsymbol{x}$을 푼다고 해봅시다. 우변을 넘기면 다음과 같이 되겠죠.

$$A \boldsymbol{x}= \lambda \boldsymbol{x}\Longrightarrow (A-\lambda I)\boldsymbol{x}=0\quad\cdots (1)$$

이 때, 식 (1)을 만족하는 모든 해 $\boldsymbol{x}$들의 집합이 $\small A-\lambda I$의 영공간(null space) 이 될 것입니다! 따라서 이 집합은 n차 실수 공간 $\mathbb{R}^n$의 부분공간(subspace) 이고, 이 부분공간을 $\lambda$에 해당하는 $A$의 고유공간(eigenspace) 이라고 부릅니다. 다시 말해서, 고유공간은 영벡터와 λ에 해당하는 모든 고유벡터들로 구성됩니다. 이제 이와 관련하여 다음의 중요한 정리(theorem)를 하나 짚고 넘어가겠습니다!

Thm. 어떤 nxn 행렬 $A$가 서로 다른 r개의 고유값 $\lambda_1, \lambda_2, \cdots, \lambda_r$을 가지고 있고, $v_1,v_2, \cdots v_r$이 이들 각각에 해당하는 고유벡터일 때, 집합 ${v_1, v_2, \cdots v_r }$은 선형독립$(linearly\space independent)$이다.

고유값들이 서로 다르면 이에 해당하는 서로 다른 고유공간이 존재하겠죠? 즉, 서로 다른 고유공간을 구성하는 고유벡터들은 서로 선형독립이라는 것입니다. 간단하게 증명해봅시다! 독립이 아니라고 가정했을 때 이 가정이 모순이 되는 것을 보이는 논리입니다.

이해되셨나요? 이제 예제를 하나 보면서 정리해보겠습니다!

• $x,y,z$ 세 축이 있을 때, $T:\mathbb{R}^3\rightarrow \mathbb{R}^3$이 $x-y$ 평면으로의 정사영 함수$(projection function)$라고 하자. 이 때 $T$에 해당하는 $transformation\space matrix\space A$의 고유값과 고유벡터를 구해보자.

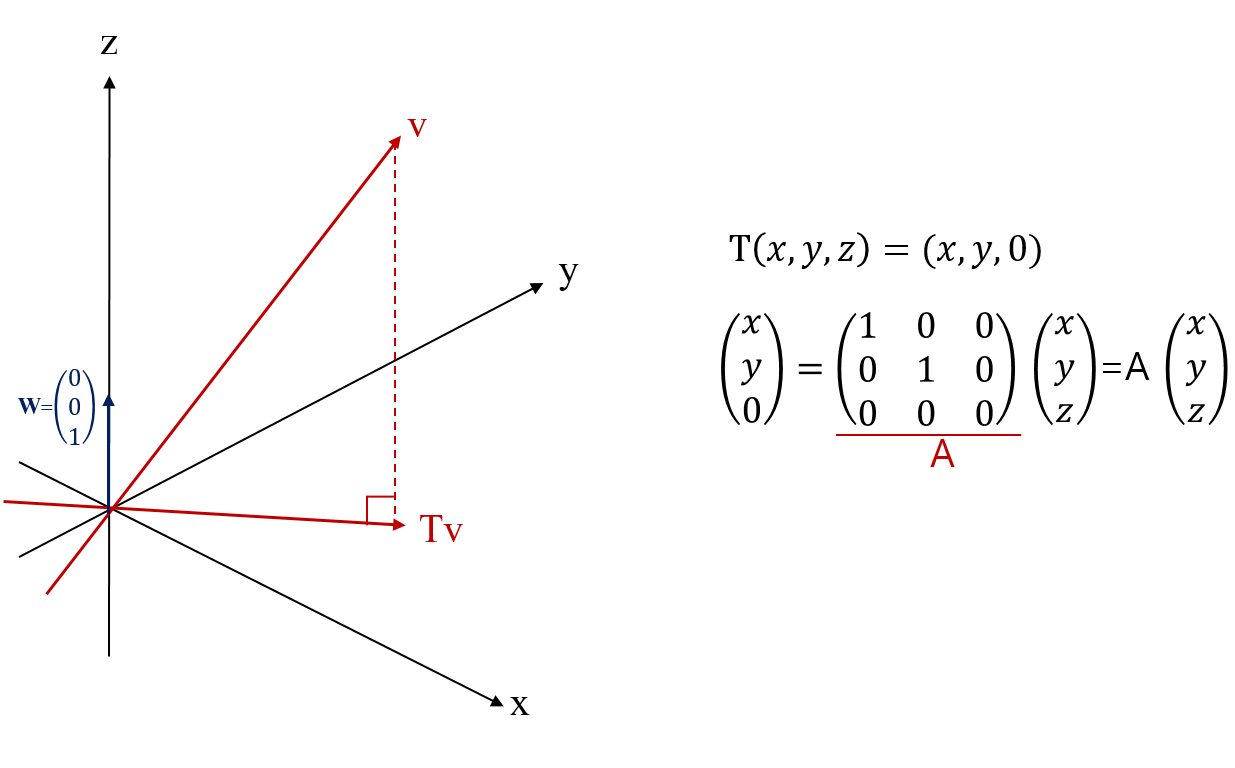
아직 포스트 순서 상 projection에 대해 접하지 않았지만, 혹시 모르시는 분들은 함수 $T$가 하는 일이 위 그림처럼 아래 바닥에다 벡터 $\boldsymbol{v}$를 그림자처럼 투영시키는 거라고 생각해주세요! 그러면 위 식과 같이 선형함수 $T$에 임의의 벡터 $(x,y,z)$를 대입한 값은 $\small T(x,y,z)=(x,y,0)$와 같이 나올 것입니다. 이제 함수 $T$를 행렬로 나타내 봅시다. $(x,y,z)$에 어떤 행렬을 곱했을 때 $(x,y,0)$이 나오는지 찾으면 됩니다. 이 예제의 경우 특별한 연산과정 없이도 간단하게 그 행렬을 찾을 수 있습니다! 위 식에서 나와있듯이, 행렬은 $\scriptsize\begin{pmatrix}1&0&0\cr 0&1&0\cr 0&0&0\end{pmatrix}$이 되고, 이를 $A$라 하겠습니다. 이렇게 어떠한 벡터를 선형함수 $T$에 대입한 값은 행렬 A와 그 벡터의 곱$\small(T(\boldsymbol{x})=A\boldsymbol{x})$으로 나타낼 수 있게 됩니다. 이제 고유값과 고유벡터를 구할 건데, 이 경우도 특별한 연산 과정이 필요 없습니다! 고유값과 고유벡터의 정의 기억하시죠? $A\boldsymbol{x}=\lambda\boldsymbol{x}$을 만족하는 $\lambda$와 $\boldsymbol{x}$를 찾아봅시다.

(1) $T(\boldsymbol w)=A\boldsymbol w=\boldsymbol 0=\boldsymbol 0\cdot \boldsymbol w$
이 때, 고유값은 0이고 그에 해당하는 고유벡터는 $\boldsymbol w=\scriptsize\begin{pmatrix}0\\0\\1\end{pmatrix}$이 되는 것을 쉽게 알 수 있습니다.
(2) $T(e_1 )=Ae_1=e_1=1\cdot e_1$ 이 때, 고유값은 1이고 그에 해당하는 고유벡터는 $e_1=\scriptsize\begin{pmatrix}1\\0\\0\end{pmatrix}$이 되는 것을 쉽게 알 수 있습니다.
(3) $T(e_2 )=Ae_2=e_2=1\cdot e_2$ 이 때, 고유값은 1이고 그에 해당하는 고유벡터는 $e_2=\scriptsize\begin{pmatrix}0\\1\\0\end{pmatrix}$이 되는 것을 쉽게 알 수 있습니다.

따라서, 고유값이 0일 때의 고유공간 은 $\scriptsize\begin{Bmatrix}\begin{pmatrix}0\\ 0\\1\end{pmatrix}\end{Bmatrix}$이 되고, 고유값이 1일 때의 고유공간 은 $\scriptsize\begin{Bmatrix}\begin{pmatrix}1\\0\\0\end{pmatrix},\begin{pmatrix}0\\1\\0\end{pmatrix}\end{Bmatrix}$ 이 되겠네요! 이 예제에서는 A의 형태가 되게 단순해서 특별한 계산과정 없이도 고유값과 고유벡터를 충분히 떠올릴 수 있었습니다. 하지만, 대부분의 경우에서 이렇게 바로 떠올리기는 쉽지 않은데요. 이 경우에는 어떻게 고유값과 고유벡터를 구할 수 있는지 알아봅시다!

2. 특성방정식(Character Equation)

특성방정식(Character Equation)이란, 단도직입적으로 $det(A-\lambda I)=0$ 을 의미합니다. 이 방정식이 왜 중요할까요? 다음의 중요한 사실(Fact)을 봅시다.

어떤 $scalar\space\lambda$가 nxn 행렬 A의 고유값이기 위한 필요충분조건은 $\lambda$가 $det(A-\lambda I)=0$을 만족하는 것이다.

즉, 위의 사실을 이용해서 우리는 복잡한(?) 행렬들에 대해서도 고유값과, 그리고 이에 해당하는 고유벡터를 계산할 수 있게 됩니다! 나아가, $\lambda$가 어떤 정방행렬 A의 고유값이기 위한 필요충분조건은 다양한 표현들로 나타낼 수 있는데요. 이들은 다음과 같습니다.

• $\lambda$는 행렬 A의 고유값이다.
  $\iff A\boldsymbol{x}=\lambda \boldsymbol{x}$를 만족하는 0이 아닌 벡터 $\boldsymbol{x}$가 존재한다.
  $\iff Nul(A-\lambda I)\not={0}$
  $\iff det(A-\lambda I)=0$
  $\iff A-\lambda I$는 역행렬이 존재하지 않는다.

위 필요충분조건의 여러가지 표현들 잘 이해가 가시나요? 앞서 배웠던 고유값과 고유벡터의 개념, 그리고 이 포스트에서는 다루지 않았지만 determinant의 성질을 생각해본다면 충분히 이해가 되실 거라 생각합니다! (참고로 $A$가 역행렬이 존재하기 위한 필요충분조건은 $det(A)\not=0$입니다.) 마지막으로, 여기서 고려해볼 점이 하나 있습니다. 만약 고유값이 0이라면 이건 어떤 의미일까요? 위 필요충분조건들에서 마지막 줄을 보면, 0이 A의 고유값이기 위한 필요충분조건은 A의 역행렬이 존재하지 않는다는 것이 될 것입니다! 이걸 조금 더 이해해봅시다. $A$가 nxn행렬이라고 할 때, $\small det(A-\lambda I)=0$을 풀어서 $\lambda$에 대한 방정식으로 나타내봅시다.

$$\begin{aligned} det(A-\lambda I)&=\lambda^n+\alpha\lambda^{n-1}+\cdots+ \beta\\ &=(\lambda-\lambda_1)(\lambda-\lambda_2)\cdots(\lambda-\lambda_n)=0 \end{aligned}$$

이렇게 구한 $\lambda_1,\lambda_2,\cdots,\lambda_n$이 A의 고유값이 됩니다. 그런데 저기서 $\beta$에 주목해봅시다. 만약 $\lambda$ 자리에 모두 0을 넣으면 $\beta$는 다음과 같이 표현이 될 것입니다.

$$det(A)=\beta=(-1)^n\cdot\lambda_1\lambda_2\cdots\lambda_n$$

그런데 여기서 고유값 중 하나가 0이 되면 어떻게 되나요? $\lambda_1,\lambda_2,\cdots,\lambda_n$중 하나라도 0인게 있다면 $\small det(A)=0$이 될 것입니다. 우리는 선형대수를 배우면서 어떤 행렬의 역행렬이 존재하는지(invertible) 아닌지의 여부를 정말 다양한 표현들로 배우게 됩니다. 고유값이 0이다도 그중 하나가 되는 것입니다!

여기까지 전반적인 고유값, 고유벡터, 특성방정식의 기초 개념에 대해서 알아보았습니다. 다음에는 대각화(Diagonalization) 에 대해 포스팅하려고 합니다. 감사합니다 :)

---

$Reference.$

• David C.Lay · Stephen R.Lay · Judi J.McDonald, Linear Algebra and its Applications, 5th edition, Pearson
• 고려대학교 김홍중 교수님의 수업