[이산형 분포] 베르누이 분포(Bernoulli distribution), 이항 분포(Binomial distribution)
이제부터 통계학에서 기본이 되는 다양한 분포들에 대해 정리하고자 합니다! 이번 포스트에서는 베르누이 분포(Bernoulli Distribution)와 이항 분포(Binomial Distribution) 에 대해 알아보고, 기대값, 분산, 그리고 적률생성함수도 구해보고자 합니다.
베르누이 분포(Bernoulli Distribution)
먼저 베르누이 시행(Bernoulli Trial)이라는 것은 ‘성공’과 ‘실패’의 두가지 결과만이 존재하는 시행으로서, 각 시행은 서로 독립 인 것을 말합니다. 대표적인 예가 동전 던지기인데요. 동전을 던지면 앞면이 나오거나 뒷면이 나오거나 둘 중 하나일 것이고, 동전을 반복적으로 던졌을 때, 먼저 시행에서 앞면이 나왔다고 그 다음 시행에서 뒷면이 나올 확률이 더 높다거나 그러지는 않을 것입니다! 다시 말해서 각 시행은 서로에게 영향을 주지 않고, 독립입니다. 앞으로 등장하게 될 이항 분포, 기하 분포, 음이항 분포 모두 베르누이 시행을 전제로 하고 있습니다!
이제 한 베르누이 시행에서, 어떤 확률변수 X가 시행의 결과가 ‘성공’이면 1이고, ‘실패’면 0의 값을 갖는다고 할 때, 이 확률변수 X를 바로 베르누이 확률변수라고 부르고, 이것의 분포를 베르누이 분포라고 합니다. 시행의 결과가 ‘성공’일 확률을 p라고 한다면, X는 $Bernoulli(p)$를 따른다고 말합니다.
\[\begin{gathered} X=\begin{cases} 1 & \text{if trial is success} \cr 0 & \text{if trial is failure} \end{cases} \cr X\sim Bernoulli(p) \cr f_X(x)=p^x(1-p)^{1-x},\space x=0,1 \end{gathered}\]확률변수의 기대값과 분산을 구하면 다음과 같이 될 것입니다. 성공할 확률 그 자체가 베르누이 확률변수의 기대값이 되는 것을 확인할 수 있습니다.
\[\begin{aligned} E(X)&=1\cdot p + 0\cdot (1-p) = p \cr Var(X) &= E(X-p)^2 \cr &=(0-p)^2\cdot (1-p) + (1-p)^2\cdot p \cr &= p(1-p) \end{aligned}\]이항 분포(Binomial Distribution)
베르누이 분포에서는 딱 시행을 한번만 한 것을 고려한 것입니다. 이 때 시행을 여러 번 했을 때가 바로 이항분포입니다! 이항분포의 확률변수 X는 베르누이 시행을 n번 했을 때, 성공한 횟수를 말합니다. 다시 말해서, 서로 독립이고 동일한 베르누이 분포를 따르는 n개의 확률변수 $X_1,\cdots , X_n$을 모두 더한 것 $X=\sum X_i$가 이항 확률변수가 됩니다. 이 때, X는 $Binomial(n, p)$를 따른다고 말합니다.
\[\begin{gathered} X \sim Binomial(n, p) \cr f_X(x)=\binom{n}{x} p^x(1-p)^{n-x}, \space x=0,1,\cdots , n \end{gathered}\]이제 이항분포의 기대값과 분산, 그리고 적률생성함수까지 구해봅시다. 이항분포는 앞서 서로 독립이고 동일한 베르누이 분포를 따르는 확률변수들을 n개 합한 것이기 때문에, 기대값과 분산은 다음과 같이 매우 간단하게 구해집니다. 적률 역시 이항정리를 이용해서 쉽게 구할 수 있습니다.
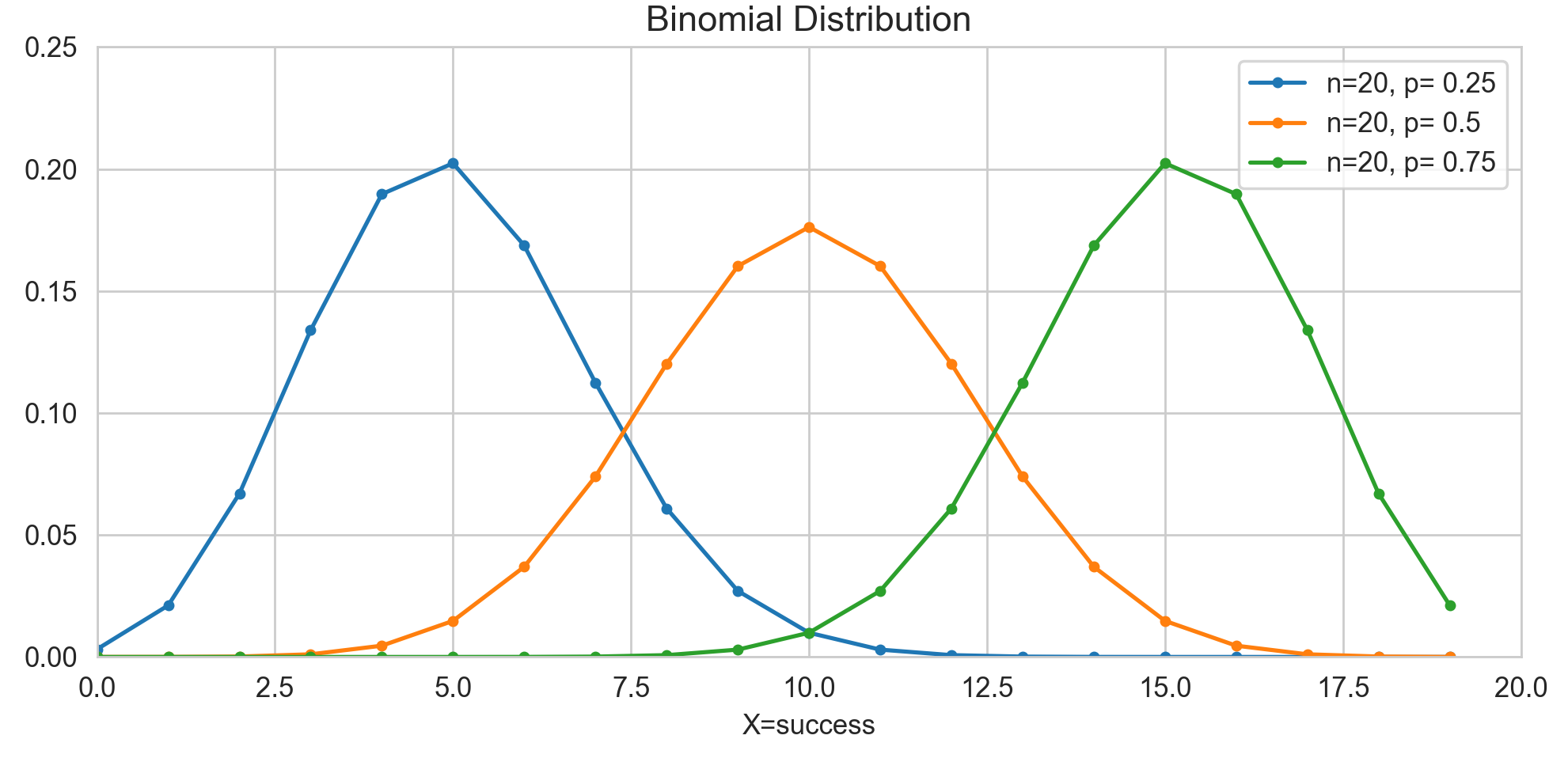
\[\begin{aligned} E(X) &= E(\sum_{x=0}^{n} X_i) = \sum_{x=0}^{n} E(X_i) =np \cr Var(X) &= Var(\sum_{x=0}^{n} X_i) = \sum_{x=0}^{n} Var(X_i) = np(1-p) \cr M_X(t) &= E(e^{tX}) = \sum_{x=0}^{n} \binom{n}{x} e^{tX} p^x(1-p)^{n-x} \cr &= \sum_{x=0}^{n} \binom{n}{x} (pe^t)^x (1-p)^{n-x} \cr &= [1-p+pe^t]^n \end{aligned}\]아래 각 성공확률에 따른 이항 분포를 확인해보면, 성공확률이 클수록 성공 횟수(X)가 많을 확률이 높은 것을 확인할 수 있습니다. 또 한, 성공확률이 중간, 즉 0.5에 가까울 수록 미세하지만 봉우리가 낮고 분산이 가장 큰 것을 확인할 수 있습니다.
앞으로 이항분포는 다른 분포들에 대한 포스트에서도 자주 등장할 예정입니다!
$Reference$
- 송성주, 전명식. (2015). 수리통계학