[머신러닝의 해석] 3편. 모델 상관없이 변수 중요도의 파악: Permutation Feature Importance | Python
이제부터는 특정 모델에 특화된(Model-specific)이 아닌, 어느 모델이든(Model-agnostic) 학습시킨 후(Post-hoc)에 적용하는 방법들에 대해 다루고자 합니다. 이번 포스트에서는 그 중에서도 변수 중요도를 확인할 수 있는 대표적인 방법 중 하나인 Permutation Feature Importance에 대해 설명하고자 합니다. Permutation Feature Importance는 Black-box 모델에 대하여, 특정 feature를 안 썼을 때, 이것이 성능 손실에 얼마만큼의 영향을 주는지를 통해 그 feature의 중요도를 파악하는 방법입니다. 이 방법의 이론은 상당히 직관적이어서 그 어떤 방법보다 이해하기 쉬운 것 같습니다. 그럼 시작하겠습니다!
Permutation Feature Importance의 특징
Permutation Feature Importance의 중요한 특징이자 장점으로는 재학습시킬 필요가 없다는 것입니다. 특정 Feature를 제거하고 모델을 재학습해서 중요도를 파악하는 방법도 있지만, 그렇게 하면 당연히 시간적, 자원적 소모가 매우 클 것입니다. 그 feature를 제거하고 예측하기 위해서는, X의 차원이 변경되어 새로 학습시켜야 하기 때문입니다. 그렇다면 특정 feature를 어떻게 안 쓰고 예측 에러를 계산할 수 있을까요? 변수를 아예 포함하지 않는 것 대신, 그 feature의 값들을 무작위로 섞어서(permutation) 그 feature를 노이즈로 만드는 것입니다! 무작위로 섞게 되면, 목표 변수와 어떠한 연결고리를 끊게 되는 것이므로, 그 feature를 안 쓴다고 할 수 있을 것입니다. 이렇게 섞었을 때 예측값이 실제 값보다 얼마나 차이가 더 생겼는지를 통해 해당 feature의 영향력을 파악합니다. 모델이 이 변수에 크게 의존하고 있을 경우에는 예측 정확도가 크게 감소할 것입니다. 이렇게 학습한 모델과 데이터만 있으면 변수 중요도를 뽑아주는 방법이기 때문에, 모델의 학습 과정, 내부 구조에 대한 정보가 필요 없어서 어느 모델이든 적용할 수 있게 됩니다.
이 방법의 또 다른 특징으로는, 각 feature의 중요도는 ‘partial importance’가 아니라는 점입니다. 각 feature의 중요도 안에는 다른 feature들과의 교호작용도 포함됩니다. 특정 feature의 값들을 랜덤으로 섞으면, 다른 feature들과의 연결고리도 끊어지게 되어, 해당 feature와 관련이 있는 모든 교호작용의 영향이 사라질 것입니다. 따라서, 두 feature 간 교호작용의 영향은 그 두 개의 feature importance 각각에 중복 포함됩니다.
주의할 점
한편, Permutation Feature Importance를 적용하기 앞서 주의해야 할 점이 있습니다. 이 방법은 값을 무작위로 섞는 것이 특징입니다. 그렇기 때문에, 할 때마다 결과가 매우 달라질 수 있습니다. 물론 이 점은 섞는 횟수를 늘림으로써 예측 에러의 분산을 감소시킬 수 있지만, feature의 개수가 매우 많을 경우에는 연산량이 증가할 것입니다. 따라서, Permutation의 적절한 횟수를 선택해야 할 것입니다.
무엇보다, 무작위로 섞다보면 매우 비현실적인 데이터 인스턴스(instance)를 생성할 가능성도 높습니다. 특히, 변수들 간 상관관계가 높을 경우 이러한 문제점이 발생하기 쉽습니다. 예를 들어, 변수 중에 ‘키’와 ‘몸무게’가 있다고 할 때, 이 두 변수들은 상식적으로 상당한 연관이 있습니다. 그런데, 키의 값들을 랜덤으로 섞다 보면, 키가 2m인데 몸무게가 30kg인 인스턴스가 만들어질 수도 있을 것입니다. 이런 사례가 충분히 있을 만한 사례라고 보기는 어렵습니다. 데이터의 이러한 비개연성, 비현실성이 증가하면, 예측값에 지대한 영향을 미칠 가능성이 있고, 이렇게 해서 중요도가 높게 나온다 해도 우리가 원하던 ‘Feature Importance’는 아닐 것입니다. 따라서, 미리 변수들 간 상관관계가 매우 높은지 확인하고, 이를 염두에 두고 결과를 해석해야 할 것입니다.
eli5 라이브러리로 적용하기
저는 파이썬 eli5 라이브러리를 이용해서 Permutation Feature Importance를 간단하게 적용해보았는데요. [머신러닝의 해석] 2편-(2). 불순도 기반 Feature Importance는 진짜 연속형 변수를 선호할까? 포스트에서 했던 데이터 Adult Census Income 에 그대로 적용했습니다. 당시에는 랜덤 포레스트만을 이용해서, 과적합 정도에 따른 랜덤 포레스트의 변수 중요도를 비교했었는데요. 이번에는 XGBoost, CatBoost, RandomForest, 총 세가지의 모델을 이용했고, 그 결과에 대한 변수 중요도를 비교해 보았습니다. 또 한, 똑같이 랜덤 포레스트 과적합 정도에 따라 Permutation Feature Importance 방법도 변수 중요도의 차이가 있는지 확인해보았습니다! 참고로, 저는 test 데이터셋에서의 변수 중요도를 확인했습니다. 아래 내용에 대한 코드는 이곳에 있습니다.
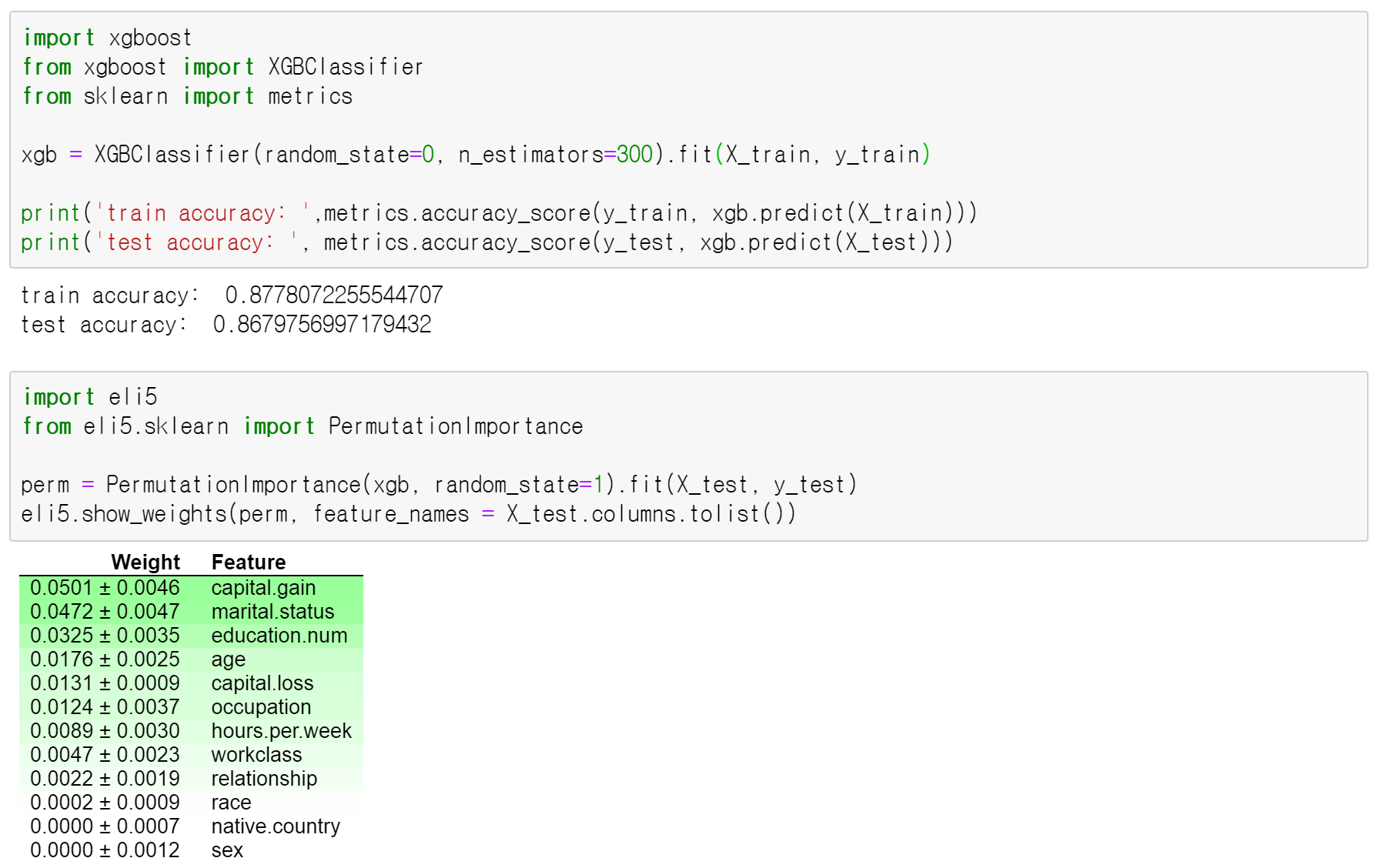
(1) XGBoost
먼저 XGBoost 모델링을 이용했을 때의 accuracy와 Permutation Feature Importance는 다음과 같습니다. (1)capital.gain, (2)marital.status, (3)education.num 세가지 변수가 상위권을 차지했습니다!
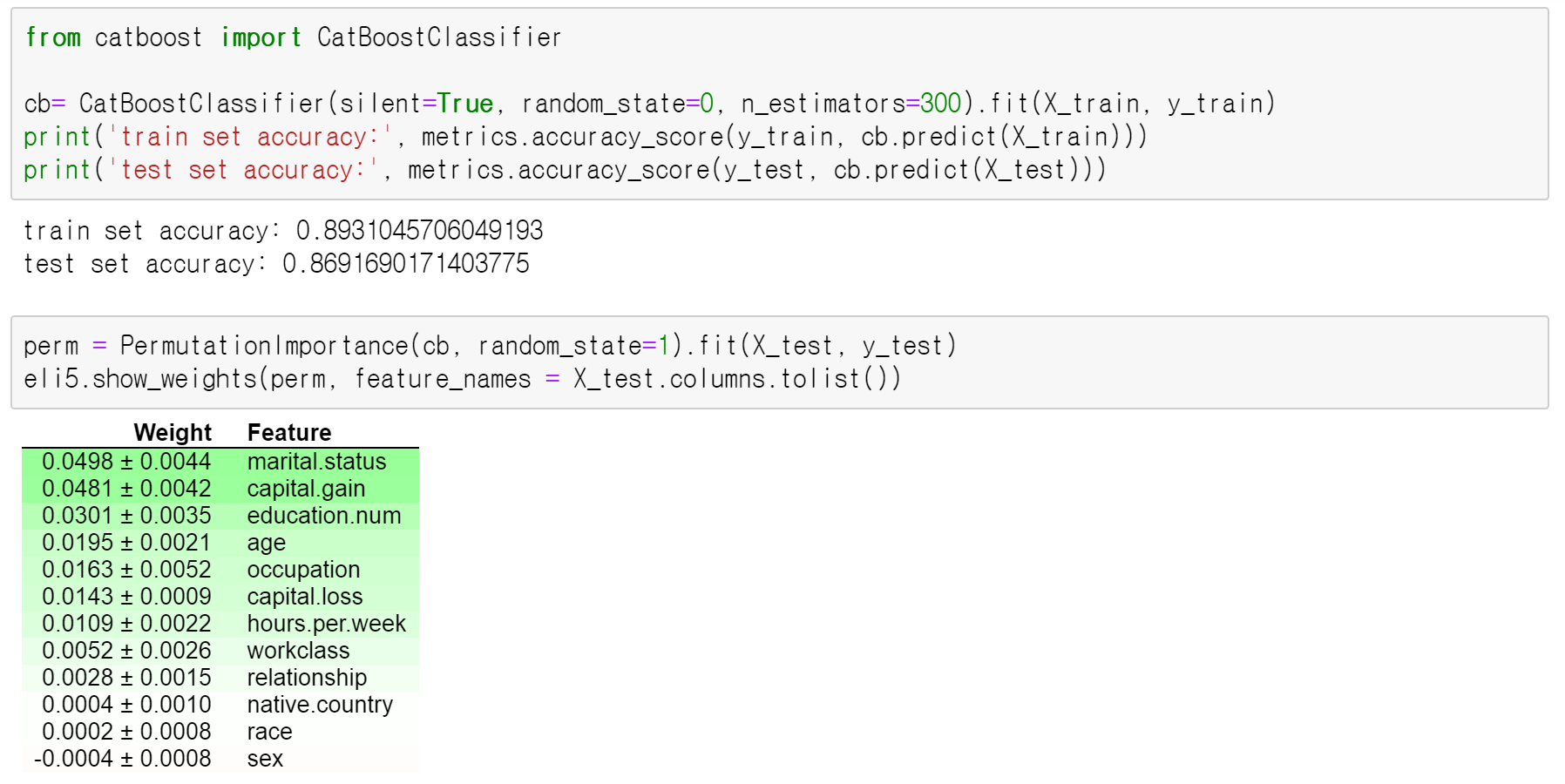
(2) CatBoost
다음은 CatBoost입니다. XGBoost와 test accuracy가 매우 비슷하고, 변수 중요도 역시 매우 비슷하지만, CatBoost에서는 가장 중요한 변수가 marital.status로 나타났습니다. 애초에, XGBoost에서도 CatBoost에서도 변수 marital.status와 capital.gain의 중요도가 큰 차이가 나지 않았다는 것을 확인할 수 있습니다. 이 점에서 두 모델 모두 상당히 비슷한 변수 중요도를 보이고 있습니다.
한편, 저번 포스트에서는 불순도 기반 변수 중요도는 모델을 과적합하게 될수록 연속형 변수의 중요도를 부풀린다는 것을 확인했는데요. 특히, 랜덤 포레스트 변수 중요도는 파라미터 max-depth정도에 따라 큰 차이를 보였습니다. Permutation Feature Imortance 역시 과적합의 정도에 따라 변수 중요도가 차이가 있는지 그대로 확인해보았습니다.
(3) RandomForest
똑같이 랜덤 포레스트 모델에 대해 (1)과적합 시킨 경우, (2)max-depth=15, (3)max-depth=10, max_depth=6일 때 변수 중요도는 다음과 같습니다.

네 경우 모두 변수 중요도가 가장 높은 상위 세 개의 변수가 같은 것을 확인할 수 있습니다. 변수 중요도가 덜 중요하게 나타날수록 순위 변동이 크게 나타나고 있습니다. 랜덤 포레스트 파라미터의 차이뿐만 아니라, 앞서 XGBoost, CatBoost 모델과도 변수 중요도가 매우 비슷하다고 볼 수 있을 것 같습니다.
불순도 기반 변수 중요도와 비교했을 때, Permutation Feature Importance는 상당히 robust한 변수 중요도를 제공하는 것 같습니다. 이번에 적용해 본 데이터에 대해서는 모델 및 파라미터에 따라 변수 중요도의 아주 큰 차이가 없다는 것을 확인할 수 있었습니다. 무엇보다, 어떤 모델이든 학습시킨 후에 간단하게 적용해볼 수 있다는 점이 매우 유용한 것 같습니다. 다만 특성 변수 개수가 훨씬 많아지면, 변수 하나하나 그 영향을 보는 과정에서 시간이 오래 걸릴 수 있을 것 같습니다.
$Reference$