[머신러닝의 해석] 2편-(2). 불순도 기반 Feature Importance는 진짜 연속형 변수를 선호할까?
저번 포스트에서 지니 불순도를 기반으로 한 트리 모델의 변수 중요도(Feature Importance)는 연속형 변수를 우대한다고 평가받는 것을 알게 되었는데요. 이러한 이유에 대해서 연속형 변수일수록 노드를 쨀 게 훨씬 많기 때문에 노드 중요도(Node Importance)가 더욱 크게 나오는 것 때문이 아닐까라고 언급했었습니다. 이번 포스트에서는 실제로 불순도 기반 변수 중요도가 연속형 변수를 우대하는지, 연속형 변수가 노드를 쨀 게 더 많아서 그런 것인지 직접 경험을 통해 알아보고자 합니다!
1. 엉터리 난수 변수가 제일 중요한 변수?
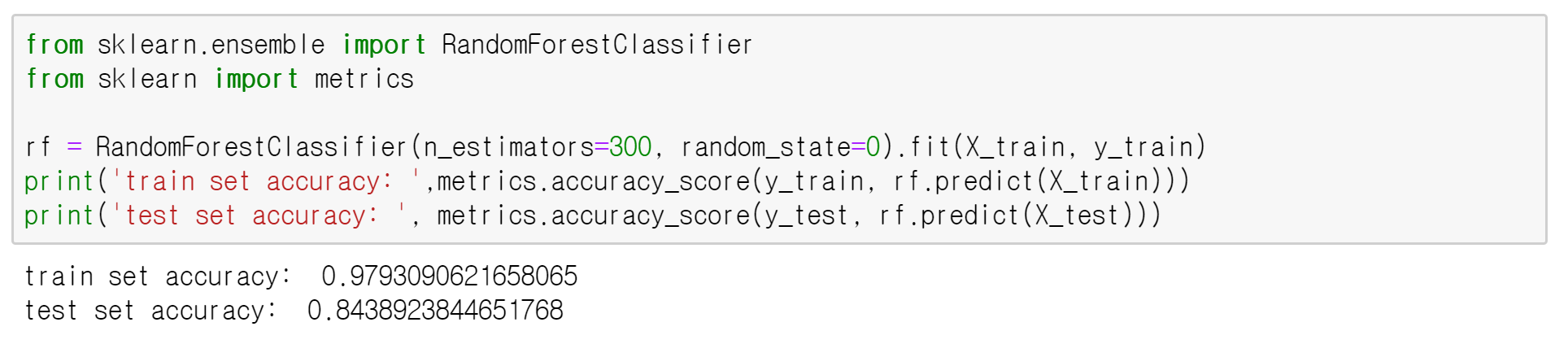
저는 처음에 Scikit-learn 공식 홈페이지에 있는 Permutation Importance vs Random Forest Feature Importance(MDI) 글에서 타이타닉 데이터에 난수로 연속형 변수를 생성하고 랜덤 포레스트를 돌렸더니, 그 엉터리 난수 변수가 랜덤 포레스트 변수 중요도가 가장 높게 나왔다는 사실을 보고 정말 놀랐었습니다. 이 장면을 목격했을 때 ‘그럼 랜덤 포레스트 변수 중요도는 믿을만하지 못한거 아냐?’ 라는 생각이 처음에 들었는데요. 조금 더 관찰해보니 모델을 과적합시켰기 때문이라는 것을 깨달았습니다. 랜덤 포레스트에 어떠한 과적합 방지를 위한 파라미터 설정도 없었고, Early Stopping 조건도 없었고, 성능도 train accuracy는 1인 반면, test accuracy는 0.817로 어느정도 차이가 존재하고 있기 때문입니다.
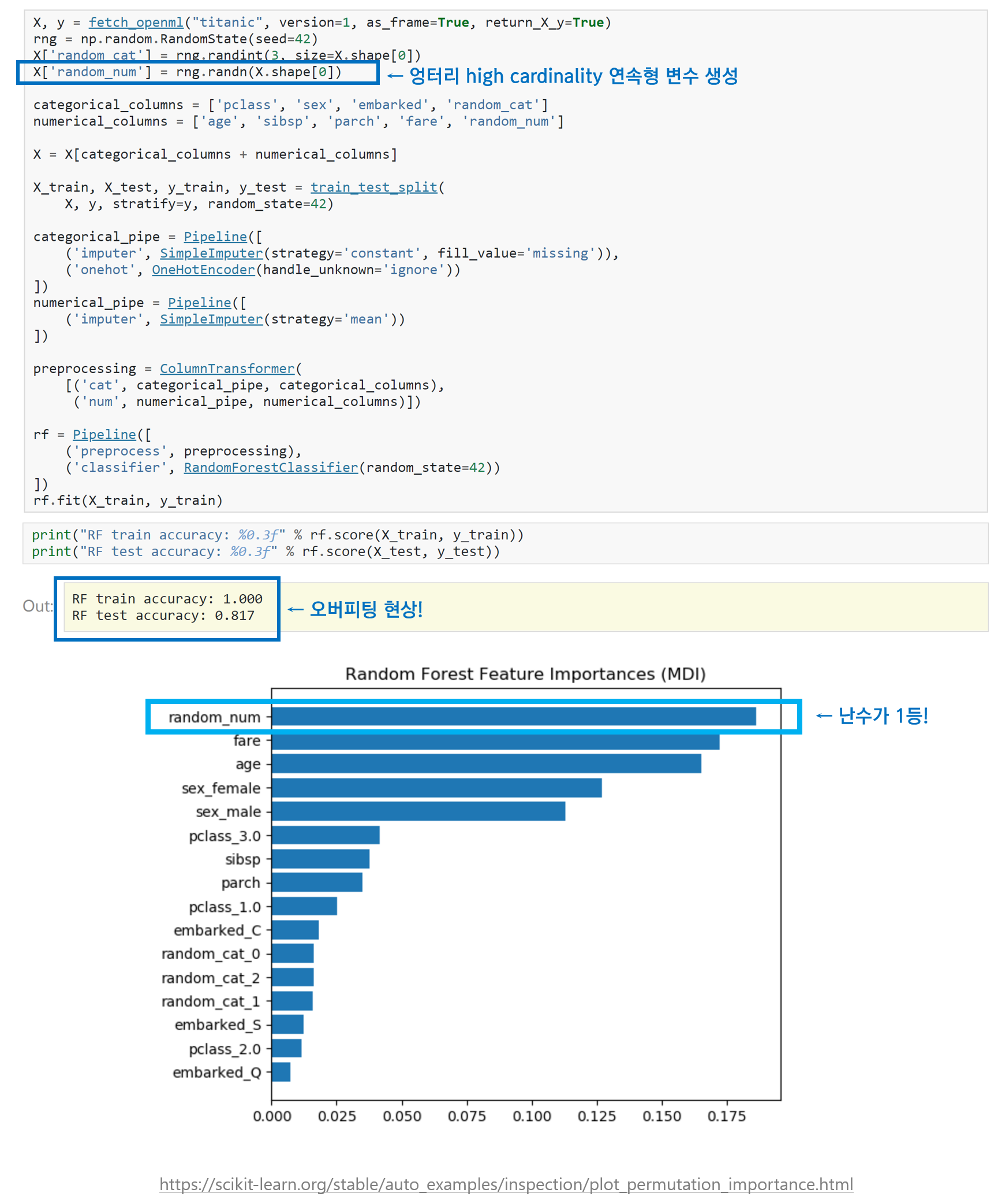
그래서 궁금해졌습니다! 과적합 시키지 않으면 어떤 결과를 뽑을까요? 중간에 멈추지 않고 끝까지 노드를 째고 째면 저런 결과가 나타나겠지만, 중간에 멈추면 다르지 않을까요? 저도 직접 해보았습니다.
2. 과적합 정도에 따른 변수 중요도 비교
(1) 데이터 소개 및 전처리
저는 UCI Machine Learning의 Adult Census Income 데이터를 이용했습니다. (데이터는 캐글에서 얻었습니다.) 이 데이터의 Target 변수와 Feature들은 다음과 같습니다.
-
Target : income(평균 연봉이 $50,000 초과면 ‘>50K’, 이하이면 ‘<=50K’)
-
범주형 변수 : Sex(2개 범주), Marital.status(3), Relationship(6), Native.country, Race(5), Workclass(8), Occupation(14), Education.num(7)
-
연속형 변수 : Hours.per.week, Capital.gain, Capital.loss, age
목적은 각 개체의 연봉이 $50,000 초과인지 이하인지 분류하는 것입니다. 이 데이터에 랜덤 포레스트 모델을 바로 적용하기 전에, 모델의 결과를 크게 변동시키지 않을 선에서 아주 약간의 전처리를 진행했습니다. 결측치를 처리하고 주요 범주형 변수들의 각 범주의 비율 차이가 심한 경우 일부 범주를 묶었습니다. 이제 본격적으로 랜덤 포레스트 모델을 적용해보고 max-depth 설정에 따라 변수 중요도가 어떻게 다른지 확인해보겠습니다! 전처리 과정과 아래 비교 실험에 대한 코드가 궁금하신 분들은 이곳을 참고해주세요!
(2) 비교 실험
-
과적합 시킨 경우
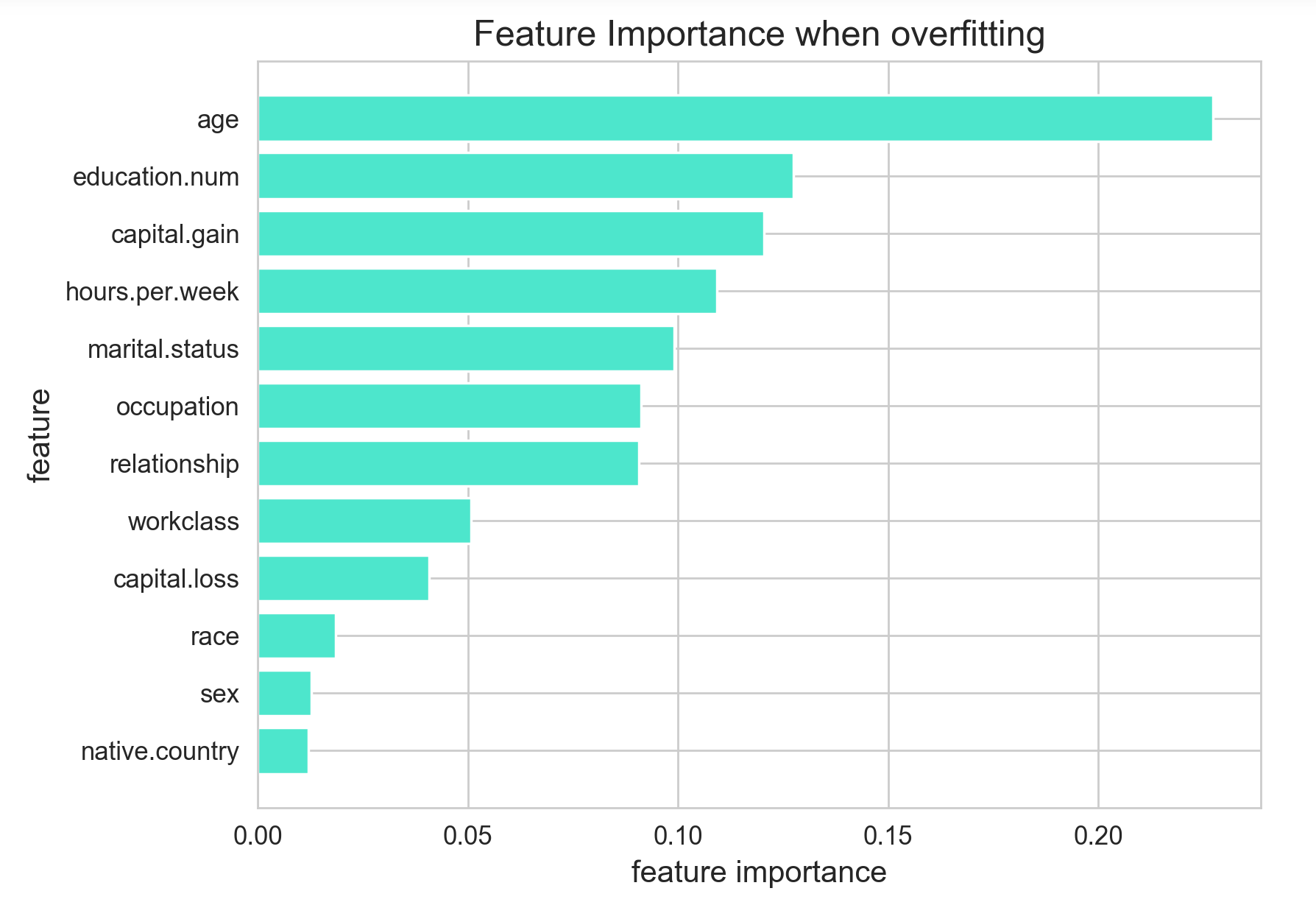
먼저 아무런 과적합 방지 조건 없이 모델을 돌린 경우입니다! train accuracy는 약 0.98인 반면, test accuracy는 0.84로, 어느정도 과적합 되었다는 것을 알 수 있습니다. 이 경우 가장 중요한 변수는 age(나이) 가 되었습니다! 나이는 당연히 high-cardinality 연속형 변수이고, 독보적으로 변수 중요도가 높은 것을 확인할 수 있습니다. 두번째로 중요한 변수 education.num 은 학력을 의미하는 변수로, 범주형이지만 범주 개수가 7개로 범주형 변수 치고 적지 않은 cardinality를 가졌습니다. (원래 데이터에서는 16개의 범주지만, 7개로 줄였습니다.) -
max_depth=15
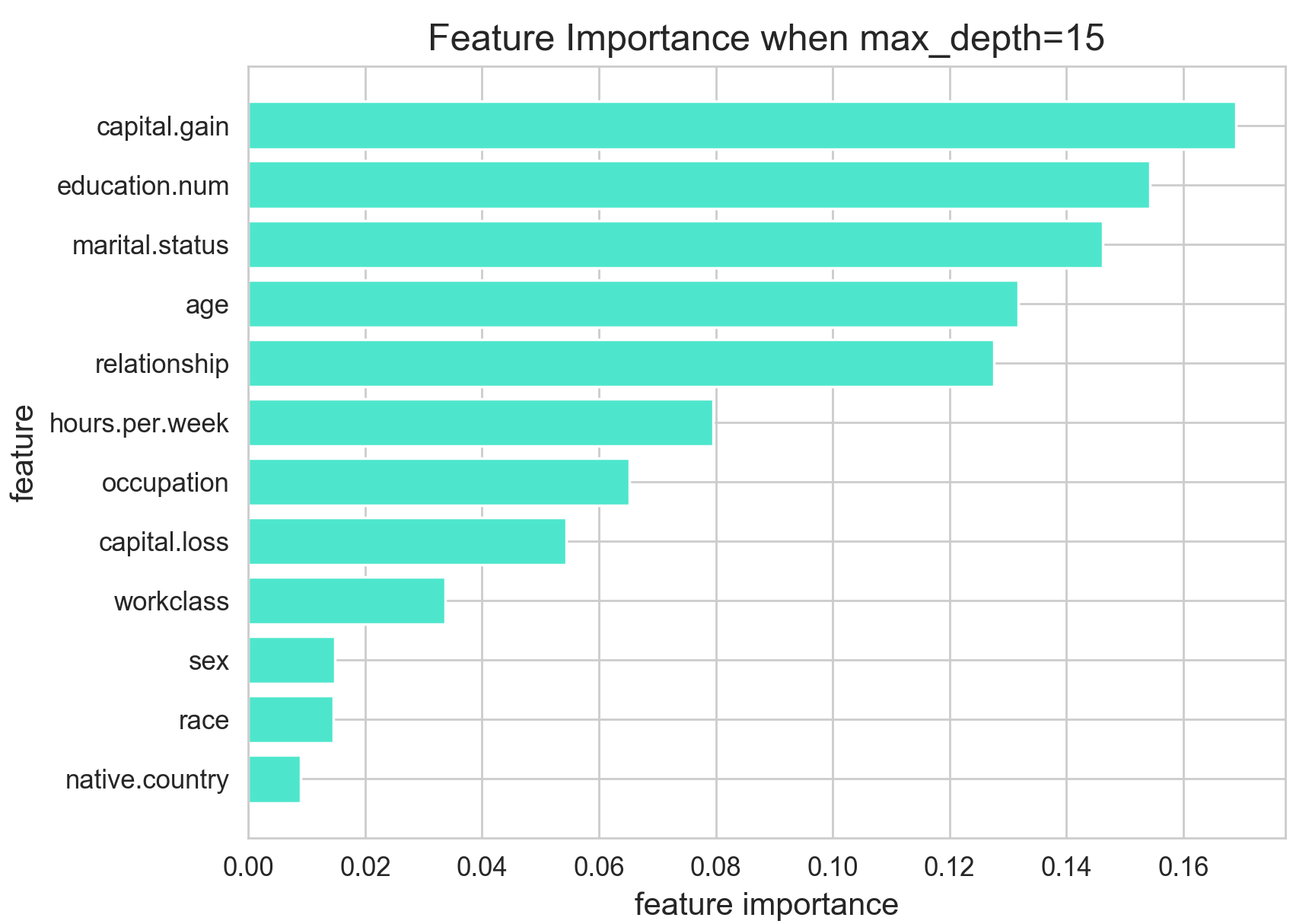
이번에는 max_depth를 15로 설정한 경우입니다. 트리의 최대 깊이를 어느정도 설정했는데요. 그 결과, 독보적으로 중요도가 높았던 age 가 4등으로 밀려났습니다. age 변수의 중요도가 급감한 것을 확인할 수 있습니다. 한편, capital.gain, 즉 자본 이득을 의미하는 또 다른 연속형 변수가 1등이 되었습니다. -
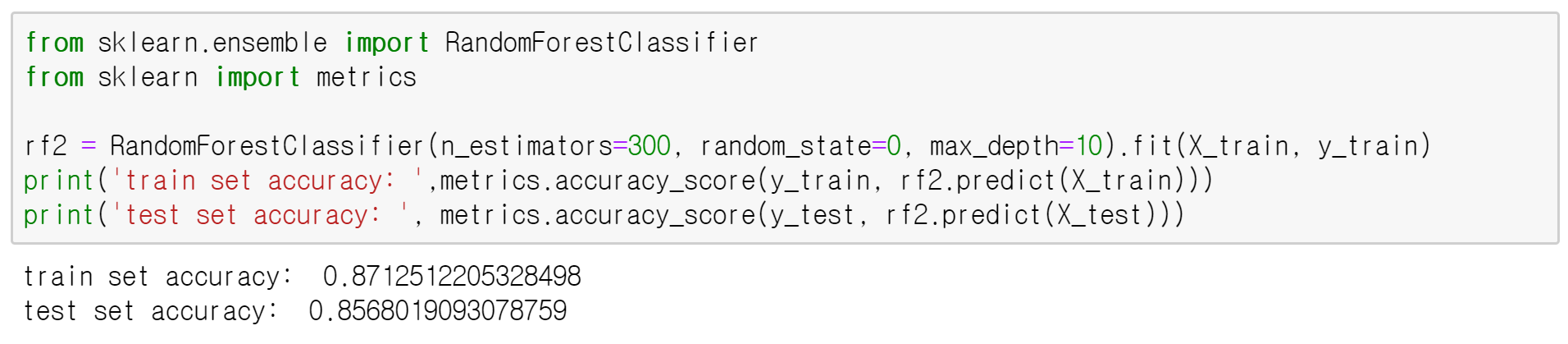
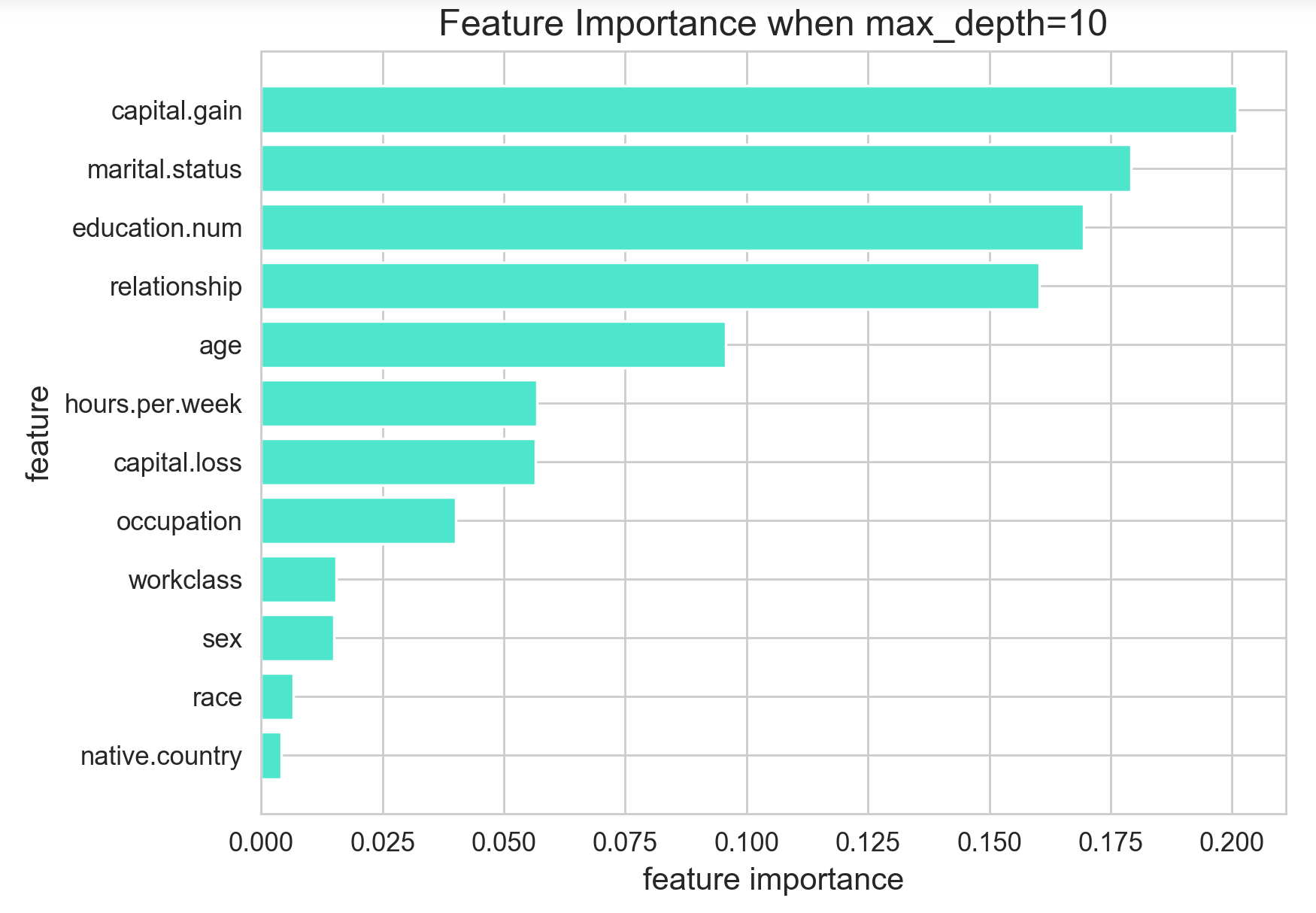
max_depth=10
max_depth를 10으로 더 낮춘 결과, 여전히 1등은 capital.gain이지만, 결혼 상태를 의미하는 marital.status 범주가 2등이 되었습니다. 이 변수는 (1)결혼 하고 같이 현재 살고 있음, (2)결혼은 했지만 같이 살고 있지 않음, (3)결혼을 안했음 으로 범주가 3개입니다. (원래 데이터에서는 범주가 5개지만, 3가지로 줄였습니다.) max_depth를 더 낮게 낮추니, low-cardinality 범주형 변수가 점차 높은 중요도를 차지하게 된 것을 확인할 수 있습니다. -
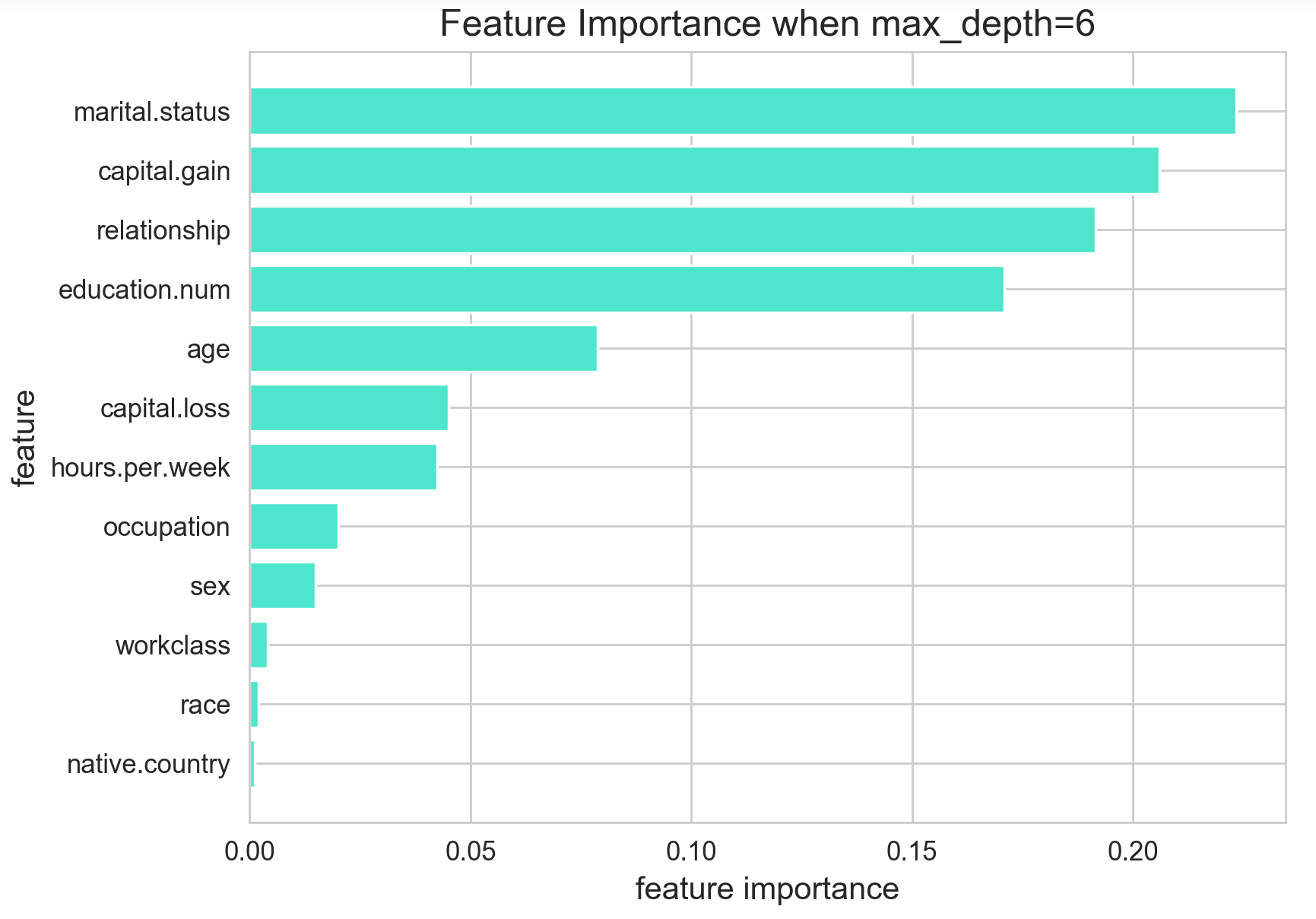
max_depth=6
마지막으로 max_depth를 6으로 낮춘 결과입니다. 이 때에는 marital.status 변수의 변수 중요도가 가장 높게 나타났습니다. 가족 관계를 의미하는 relationship 범주형 변수도 처음에 비해 많이 올라온 것을 확인할 수 있습니다.
3. 결론
트리의 과적합 방지 정도에 따라 불순도를 기반으로 하는 변수 중요도는 큰 차이를 보이는 것을 확인할 수 있었습니다. 트리가 노드를 째는 것을 중간에 멈추지 않을 경우에는 연속형 변수일수록, cardinality가 클수록 노드 중요도가 매우 커진다는 것을 알 수 있습니다. 그래서, 불순도 기반 변수 중요도는 모델을 과적합 시키지 않는 선에서는 좋은 참고 자료가 될 수 있을 것이라 생각합니다. ‘이렇게 parameter 하나하나에 따라 변수 중요도가 차이가 나면 신뢰할만 하지 못한거 아닌가?’라고 볼 수도 있지만, 각 parameter에 따라 변수 중요도가 어떻게 차이나는지까지 확인하게 되면, 이 나름의 정보를 얻게 되는 것 같습니다. 예를 들면, parameter 변경에도 불구하고 항상 상위권을 유지하는 변수들은 어느정도 변수 중요도가 높은 변수라고 볼 수 있을 것입니다. 아무래도 이러한 큰 변동성, 그리고 저번 포스트에서 언급했던 것과 같은 한계점들이 존재하긴 하지만, 트리에 특화된 이 불순도 기반 변수 중요도는 다른 방법을 따로 적용할 필요가 없고 빠르다는 점에서, 다른 방법을 통해 얻은 변수 중요도와 비교할 수 있는 좋은 대조군이라 생각합니다.
한편, 위 비교 실험에서 test accuracy가 가장 높았을 때는 max_depth=15 로 설정한 경우였습니다. 아무래도 성능이 가장 높으니, 이 때의 변수 중요도를 가장 신뢰해야 하는 것이 아닌가 싶기도 합니다. 이 때의 변수 중요도를 우선적으로 믿을지 여부를 판단하기 위해서는 다른 방법으로 모델을 해석하고 변수 중요도를 뽑아서 이것과 비교해보면 될 것입니다. 다음 포스트에서는 Model-specific 방법이 아니라, Model-agnostic 방법 중 하나인 Permutation Feature Importance에 대해 알아보고, 똑같은 데이터에 대해 변수 중요도 결과를 비교해보고자 합니다. 이번 포스트에서 확인한 대로, 범주형 변수 marital.status와 연속형 변수 capital.gain이 중요한 변수로 계속 뽑히는지 확인해봅시다!