[머신러닝의 해석] 2편-(1). 트리 기반 모델의 Feature Importance 속성

About Interpretable Machine Learning

제가 이 Interpretable Machine Learning 시리즈를 포스팅한 계기가 어쩌면 바로 이번 포스트에서 할 내용이라고 할 수 있습니다! 파이썬 모듈로 Random Forest와 같은 주요 트리 기반 앙상블 모델을 이용할 때, 모델 자체에 Feature Importance 속성이 존재해서 특별한 과정 없이도 중요한 변수들을 한눈에 볼 수 있습니다. 그런데 문득 이 변수 중요도(Feature importance)를 믿을 수 있는가에 대한 고민이 들었습니다. 고민이 들었던 이유는 제가 이 모델이 어떻게 변수 중요도를 추출하는지 몰랐기 때문입니다. 모든 데이터와 모델에 항상 완벽하게 통하는 방법은 없다 해도, 어떻게 중요도를 뽑는지는 알아야 적절히 참고해서 잘 이용할 수 있을 것입니다. 때문에, 이번 포스트에서부터는 모델의 해석 및 변수 선택을 위해 많은 사람들이 사용하는 주요 방법들에 대해 알아보고 경험해보고자 합니다! 먼저 이번 포스트에서는, 트리 기반 모델에 특화된(Model-specific) 변수 중요도 추출 방법에 대해 알아보고자 합니다. 특히 파이썬 모듈 Scikit-learn의 알고리즘을 기준으로 설명하고자 합니다.


1. 의사결정나무, CART, 불순도


의사결정나무(Decision Tree)는 그 시각적인 구조 덕분에 depth가 크지 않는 한 해석이 용이한, 간단한(simple) 모델에 해당합니다. 다른 간단 모델인 Linear Regression, Logistic Regression은 feature와 target이 선형적 관계일 때 통하는 방법인 반면, 의사결정나무는 비선형적인 관계에서도 통하는 방법이라는 점에서 매우 유용합니다. 또 한, 많은 성능 좋은 앙상블 모델들이 의사결정나무를 기반으로 하고 있습니다.

의사결정나무의 알고리즘에는 ID3, C4.5, CART 등이 있지만, 그 중에서도 Scikit-learn에서는 최적화된 CART 알고리즘을 이용한다고 합니다. CART(Classification and Regression Tree)는 각 노드가 2개의 child 노드를 가지는 binary tree를, 적절한 불순도(impurity) 지표를 기준으로 생성해 나가는 알고리즘입니다. 목적이 분류(Classification)일 때에는 불순도 지표로 Gini 계수 및 엔트로피를 이용하고, 목적이 회귀(Regression)일 때에는 MSE(Mean Square Error) 등을 이용해서 분산을 감소시키는 방향으로 노드를 째게 됩니다. 이 과정에서, 불순도를 가장 크게 감소시키는 변수의 중요도가 가장 크게 됩니다. CART 알고리즘은 바로 이 불순도를 이용해서 가장 중요한 변수들을 찾아냅니다.


2. Gini Importance


Scikit-learn에서는 지니 중요도(Gini Importance)를 이용해서 각 feature의 중요도를 측정합니다. 그 전에 지니 불순도(Gini Impurity)에 대해 살짝 짚고 넘어가겠습니다. Class가 총 $K$개 있고, 각 샘플이 해당 class에 속할 확률을 각각 $p_i, i=1,\cdots, K$라고 할 때, 특정 노드 $N_j$에서 지니 불순도는 다음과 같이 표현됩니다.

\[G(N_j)=\sum^{K}_{i=1} p_i(1-p_i) = 1-\sum^{K}_{i=1} p_i^2\]

해당 노드에서 샘플들이 이질적으로 구성되어 있을수록, 다시 말해서 모든 Class에 골고루 분포되어 있을수록 지니 불순도(impurity)는 높아지게 됩니다. 의사결정나무는 이렇게 불순도를 감소시키는 방향으로 노드를 생성하고 분류를 진행합니다. 이제 아래 간단한 예시를 한번 보겠습니다!

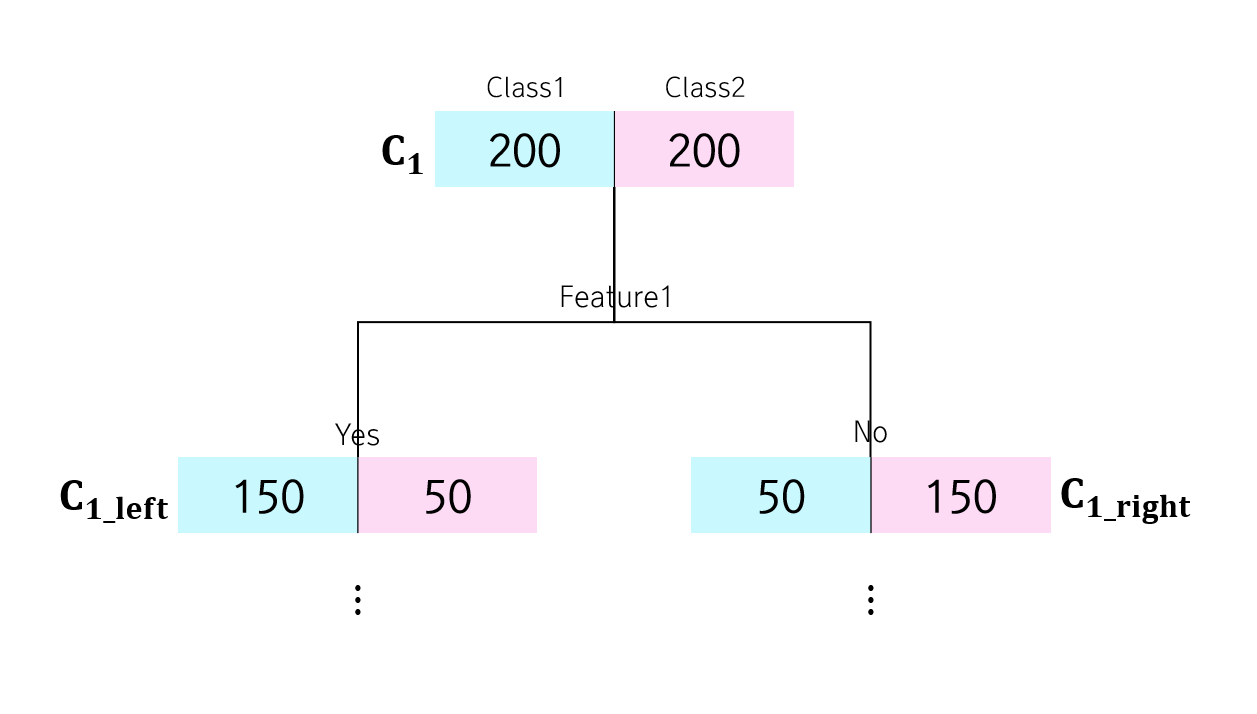
총 샘플이 400개이고, Class가 두 종류, 즉 이항 분류하는 경우입니다. 이 때, 아래 세가지 노드 $C_1, C_{1_ left}, C_{1_ right}$의 지니 불순도 $G$를 계산하면 다음과 같습니다.

\[\begin{aligned} G(C_1)&=1-\lbrace(\frac{200}{400})^2+(\frac{200}{400})^2\rbrace=0.5 \cr G(C_{1\_left})&=1-\lbrace(\frac{150}{200})^2+(\frac{50}{200})^2\rbrace=0.25 \cr G(C_{1\_right})&=1-\lbrace(\frac{50}{200})^2+(\frac{50}{200})^2\rbrace=0.25 \end{aligned}\]

$C_1$ 노드보다 그 아래에 있는 노드들의 불순도가 더 적은 것을 확인할 수 있습니다. 직관적으로 두 클래스가 골고루 섞인 것이 아니라 비교적 한 클래스에 몰빵된 형태가 되었으니, 순도(homogeneity)가 증가했다고 볼 수 있습니다. 이제 이 지니 불순도를 이용해서 각 feature의 중요도를 계산할 건데요. 그 전에 Scikit-learn에서는 각 노드의 중요도(Node Importance)를 다음과 같이 먼저 계산합니다!

$I(C_j)$는 노드 $C_j$의 중요도(Importance)를 의미하고, $w_j$는 전체 샘플 수에 대한 노드 $C_j$에 해당하는 샘플 수의 비율, 즉 가중치를 의미합니다.

\[I(C_j)=w_j\cdot G(C_j) – w_{j\_left}\cdot G(C_{j\_ left}) – w_{j\_right}\cdot G(C_{j\_right})\]

즉, 부모 노드의 가중치 불순도에서 자식 노드들의 가중치 불순도 합을 뺀 것입니다. 위 예시에서 $I(C_j)$를 계산해보면 다음과 같습니다.

\[\begin{aligned} I(C_j)&=1\cdot G(C_j) – \frac{200}{400}\cdot G(C_{j\_ left}) - \frac{200}{400}\cdot G(C_{j\_ right})\cr &=0.5-0.5\cdot 0.25 – 0.5\cdot 0.25 \cr &= 0.25 \end{aligned}\]

노드 중요도라는 게 사실 우리한테 더 잘 알려진 Information Gain을 결국 말합니다. 실제로 의사결정나무에서는 그 때 Information Gain을 최대화하는 feature를 기준으로 노드를 째게 됩니다. 어떤 노드의 노드 중요도 값이 클수록, 그 노드에서 특히 불순도가 크게 감소한다는 것을 의미하기 때문에, 이러한 면에서 그 노드가 중요하다고 말하는 것은 합리적으로 보입니다! 이제 각 feature의 중요도를 계산해보겠습니다. $i$번째 feature, $f_i$의 중요도 $I(f_i)$는 다음과 같이 계산됩니다.

\[I(f_i)=\frac{\sum_{ j: f_i에\space 의해\space split된\space 모든 노드\space C_j} I(C_j)}{\sum_{ k\in all\space node\space C_k}{I(C_k)}}\]

즉, 전체 노드의 중요도를 합한 것 대비 $i$번째 feature에 의해 째진 노드들의 중요도를 합한 것이 바로 $i$번째 feature의 중요도 $I(f_i)$가 됩니다! 이 값이 클수록, 해당 feature가 트리를 생성하고 샘플을 분류하는데 큰 역할을 했다고 볼 수 있을 것입니다. 이 $I(f_i)$를 다시 모든 feature들의 중요도의 합으로 나눠서 정규화한 것으로 이용한다고 합니다.

\[I(f_i)^{norm}=\frac{I(f_i)}{\sum_{ i \in \space all\space feature\space f_i} I(f_i)}\]

여기까지 의사결정나무의 변수 중요도였습니다. 그렇다면, 랜덤 포레스트에서 변수 중요도는 어떻게 될까요? 랜덤 포레스트는 의사결정나무들을 병렬적으로 합한 것이므로, 랜덤 포레스트에서 $I(f_i)$는 결국 각 트리에서의 $I(f_i)$를 모두 평균 낸 것에 해당합니다!


3. 불순도 기반 Feature Importance의 한계


지금까지 트리가 어떻게 지니 불순도를 이용해서 각 변수의 중요도를 계산하는지 알아보았습니다. Scikit-learn으로 의사결정나무, 랜덤 포레스트 모델을 이용할 때 참고했던 Feature Importance가 바로 이렇게 해서 얻어진 것입니다! 저는 이러한 이론을 배우고 ‘그럼 랜덤 포레스트가 출력하는 변수 중요도는 꽤 신뢰할 만 한 거 아닌가?’라고 생각을 했었는데요. 왜냐하면 각 트리들을 샘플도, 변수들도 랜덤으로 뽑아서 생성한 것을 몇백개 이상 합쳐서 얻은 변수 중요도는 충분히 신뢰할 만한 것으로 느껴졌습니다.

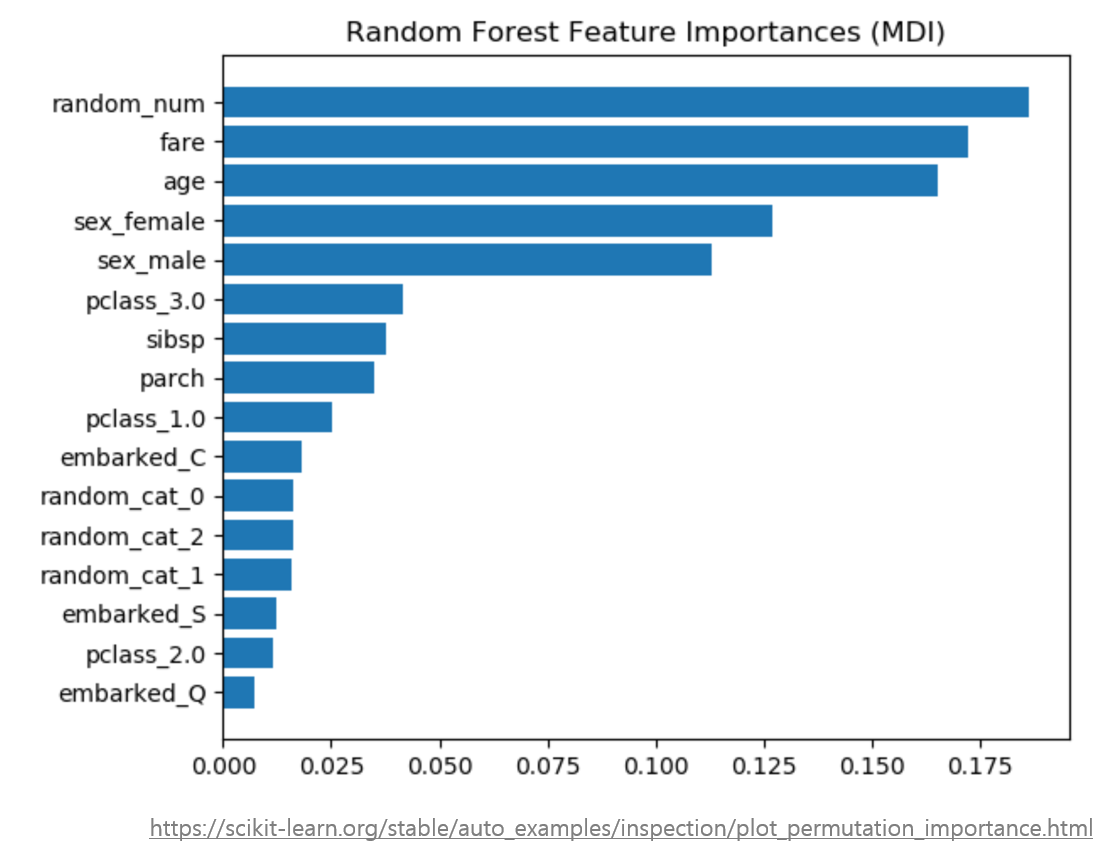
그런데 찾아보니 ‘Scikit-learn의 디폴트 랜덤 포레스트 Feature Importance는 다소 biased하다’고 합니다! 특히, 랜덤 포레스트는 연속형 변수 또는 카테고리 개수가 매우 많은 변수, 즉 ‘high cardinality’ 변수들의 중요도를 더욱 부풀릴 가능성이 높다고 합니다. 왜 이런 결과가 나오는지는 정확히 알 수 없으나, cardinality가 큰 변수일 수록, 노드를 쨀 게 훨씬 더 많아서 노드 중요도 값이 높게 나오는 게 아닐까 싶습니다. 2-(2)편에서 이에 대해 더욱 알아보겠습니다. 아무튼, 이 때문에 무조건 디폴트 Feature Importance 결과를 믿는 것 보다는, Permutation Feature Importance와 같은 다른 방법을 혼합해서 사용하는 것이 더욱 추천된다고 합니다.

또 한, 이 불순도를 기반으로 한 변수 중요도는 데이터를 학습하는 과정에서 얻은 결과입니다. 다시 말해서, train 데이터셋으로부터 얻은 통계량으로 계산된 중요도이기 때문에, test 데이터셋에서는 이 변수 중요도가 어떻게 변하는 지 알 수 없습니다. 실제로 test 데이터셋에서는 안 중요한 변수가 학습 과정에서는 가장 중요한 변수로 계산될 수 있는 것입니다.


$Reference$