[선형대수] Gram-Schmidt Process, QR Decomposition
안녕하세요! 이번 포스트에서는 그람슈미트 과정(Gram-Schmidt Process) 과 QR 분해(QR Decomposition) 에 대해 제가 배웠던 내용을 정리하고자 합니다. 바로 시작하겠습니다 😊
1. 그람슈미트 과정(Gram-Schmidt Process)
이전 포스트에서 Orthogonal Projection 을 잘 이해하셨다면, 그람슈미트 과정(Gram-Schmidt Process) 은 매우 쉽게 느껴지실거에요! 일단 그람슈미트의 요체는 다음과 같습니다. 어떤 실수 부분공간의 기저(basis)를 input으로 했더니, orthogonal 또는 orthonormal basis가 output이 되었습니다.

한마디로 어떤 부분공간을 생성하는 선형독립인 벡터들을 직교하는 벡터들로 만들어주는 과정인 것이죠. 이걸 왜 할까요? 저번 글에서 말씀드렸지만, 직교성을 갖는 기저는 많은 연산 과정에서 편리하다는 장점이 생기기 때문입니다. 특히, 직교 기저에 의해 생성되는 공간의 벡터들은 특정한 가중치들을 가진 선형결합으로 쉽게 표현 가능합니다. 이제 과정에 대해서 알아봅시다. 아래 그림을 볼까요?
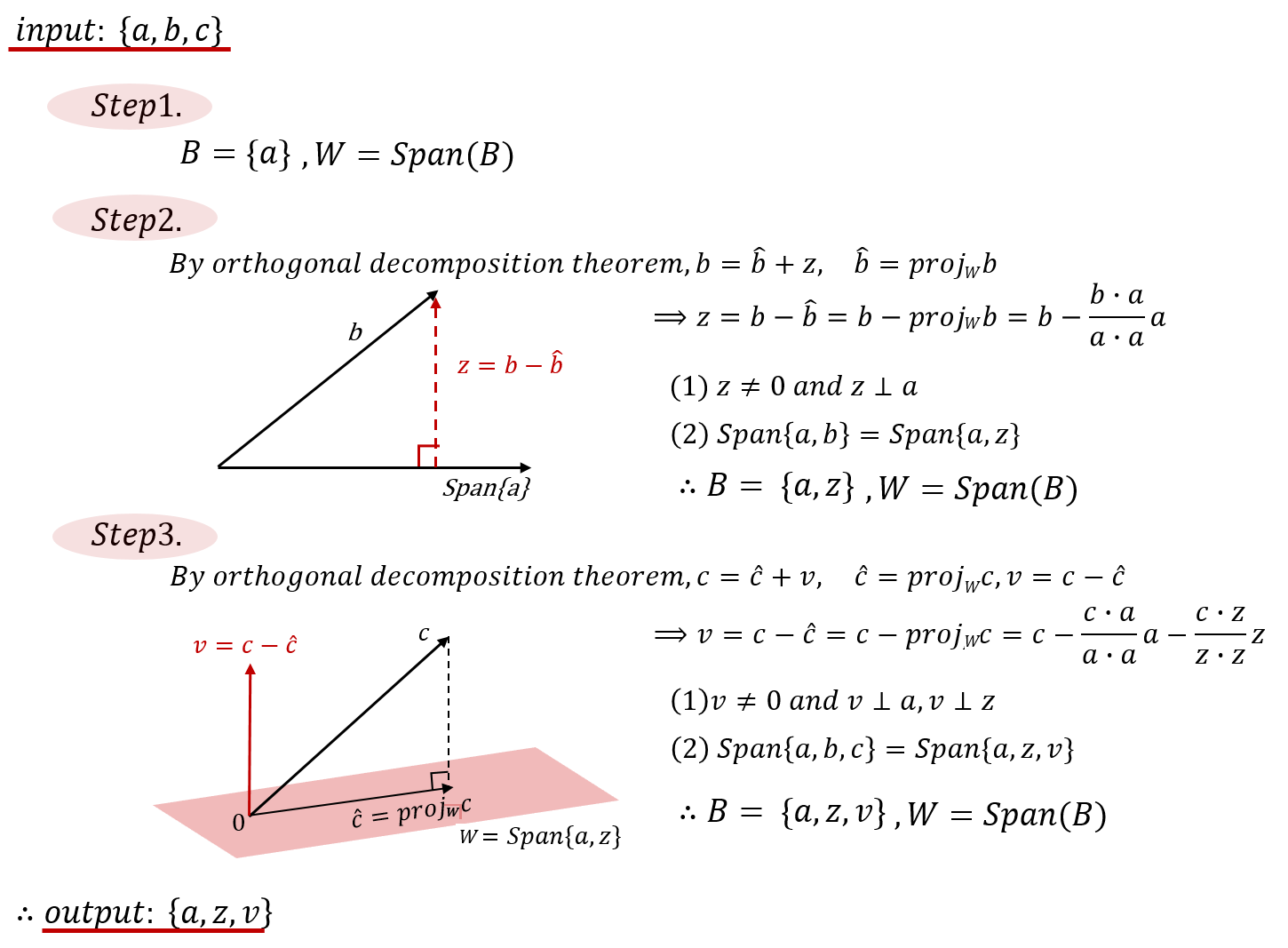
$\mathbb{R^3}$의 어떤 부분공간의 기저가 $\lbrace a,b,c\rbrace $라고 합시다. 직교 기저(Orthogonal basis)가 될 새로운 기저를 $B$라고 할 때, 첫번째 단계에는 아무 벡터나 넣습니다. 위 그림에서와 같이 벡터 $a$를 넣었다고 합시다. 두번째 단계에서 벡터 $b$를 포함하고 싶은데 $b$는 $a$와 선형 독립(linearly independent)일 뿐이지 직교하지는 않습니다. 그러면 $a$와 직교인 벡터를 어떻게 구하면 될까요? 이전에 배웠던 Orthogonal Decomposition Theorem 을 이용해서 $b$를 $Span\lbrace a\rbrace$에 정사영시킨 벡터와 $Span\lbrace a\rbrace$와 직교인 벡터성분으로 분해하면, $a$와 직교하는 벡터를 구할 수 있게 됩니다! 따라서, $a$와 직교하는 벡터 $z=b-\hat b$ 가 직교 기저 $B$의 두번째 멤버가 됩니다.
세번째 단계도 똑같이 진행합니다. $B$의 세번째 멤버는 $B$의 이미 확정된 멤버들인 벡터 $a, z$가 구성하는 평면과 직교하는 벡터라는 자격조건이 필요할 것입니다. 마찬가지로, Orthogonal Decomposition Theorem 을 이용하여 벡터 $c$를 $a,z$가 구성하는 평면에 정사영시킨 벡터와, 이 평면에 직교하는 벡터로 분해합니다. 따라서, $a, z$와 직교하는 벡터 $v=c-\hat c$ 가 직교 기저 $B$의 마지막 멤버가 됩니다.
그런데 새로 도출한 벡터들이 서로 직교한다는 것은 알겠는데, 이 부분공간의 기저라고 할 수 있을지에 대해서는 아직 물음이 남아있을 수 있습니다. 새로 도출한 직교 벡터들의 집합이 생성하는 공간이 주어진 부분공간과 같다고 할 수 있을까요? 다시 말해서, $\small Span(\lbrace a,b,c\rbrace)=Span(\lbrace a,z,v\rbrace)$이라고 할 수 있을까요? 제가 이해한 방식은 다음과 같습니다. 우선 첫번째 단계에서는 자명하게 같을 것입니다. 두번째 단계에서 $\small Span(\lbrace a, b\rbrace)=Span(\lbrace a, z \rbrace)$인지 확인해 봅시다. 일단 벡터 $a$와 $b$는 선형독립이기 때문에 일직선 상에 존재할 수 없습니다. 따라서 $\lbrace a, b\rbrace$는 어떠한 평면을 구성할 것입니다. 현재는 이 평면을 구성하는 구성원들이 직교가 아니기 때문에 비슷한 역할을 하는 부분이 존재합니다. 이제 이 구성원들을 서로 완전히 다른 역할을 하는 구성원들로 바꾸고자 합니다. (즉, 기저를 직교 기저로 표현하고자 합니다.) 그러기 위해서는 $b$에서 $a$와 관련 있는 부분을 아예 제거하면 $\small Span\lbrace a, b\rbrace$을 구성하면서 직교인 기저를 구할 수 있을 것입니다. 이를 위해 위에서 벡터 b를 벡터 a가 생성하는 공간에 존재하는 벡터와 이 공간에 직교하는 벡터 z로 쪼갠 것입니다! 벡터 $z$는 $\small Span\lbrace a\rbrace$와 직교하고, 벡터 $b$는 $\small\lbrace a, z\rbrace$가 생성하는 평면에 존재합니다. 따라서 $\small \lbrace a, b\rbrace$가 생성하는 평면과 $\small \lbrace a,z\rbrace$가 생성하는 평면은 같습니다만, $z$는 $b$에서 $a$와 관련있는 부분을 아예 제거한 것 뿐이라고 생각할 수 있습니다. 세번째 단계도 마찬가지입니다. 따라서, $\small Span(\lbrace a,b,c \rbrace)$와 $\small Span(\lbrace a,z,v \rbrace)$은 같습니다.
여기까지가 그람슈미트의 목적과 과정이었습니다. 이제 이것을 $\mathbb{R^n}$의 p차원 부분공간 $W$에 대하여 일반화하면 다음과 같습니다.

2. QR 분해 (QR Decomposition)
다음은 QR 분해(QR Decomposition)입니다. 여러가지 방법으로 QR 분해를 할 수 있는데, 그 중 하나가 그람슈미트 과정 입니다. 일단 QR분해 정리는 다음과 같습니다.
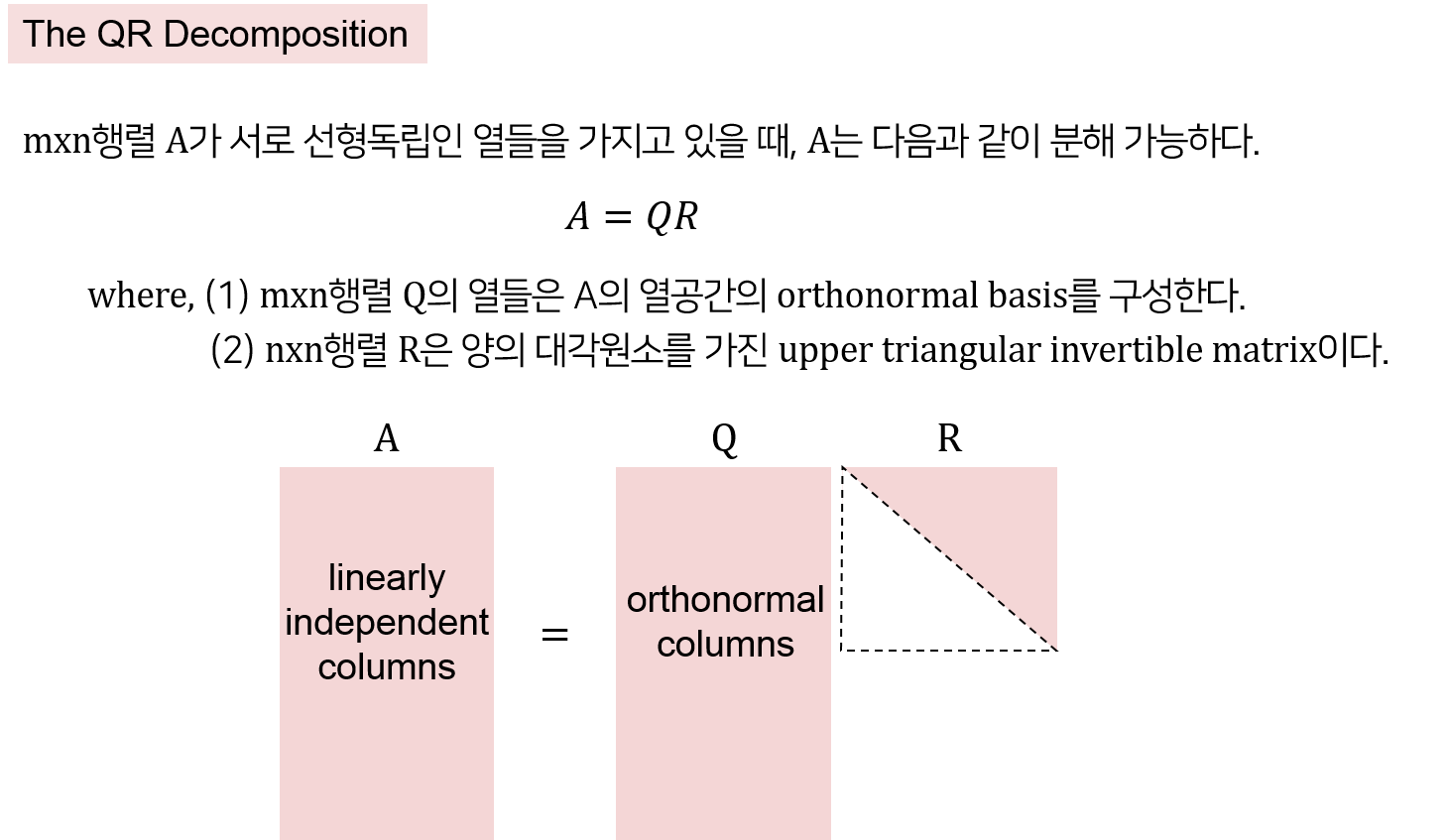
예를 들어, nx3 행렬 $A$의 열(column)들의 집합 $\lbrace x_1,x_2,x_3\rbrace$들이 서로 선형 독립 이고, 그람 슈미트 를 이용하여 구한 이 열공간에 대한 직정 기저(orthonormal basis)가 $\small\lbrace u_1=\frac{v_1}{\lVert v_1\rVert}, u_2=\frac{v_2}{\lVert v_2\rVert}, u_3=\frac{v_3}{\lVert v_3\rVert} \rbrace$ 이라고 합시다. 그람 슈미트를 이용하여 다음과 같이 직교/직정 기저를 구했을 것입니다.
\[\begin{aligned} v_1&=x_1\\v_2&=x_2-(x_2\cdot u_1)u_1\\v_3&=x_3-(x_3\cdot u_1)u_1-(x_3\cdot u_2)u_2 \end{aligned}\] \[\Rightarrow u_1=\frac{v_1}{\lVert v_1\rVert}, u_2=\frac{v_2}{\lVert v_2\rVert}, u_3=\frac{v_3}{\lVert v_3\rVert}\]이렇게 구한 직교/직정 벡터들을 가지고 역으로 원래의 벡터를 재구성해봅시다.
\[\begin{aligned} x_1&=v_1=\lVert v_1\rVert u_1 =(x_1\cdot u_1)u_1\\ x_2&=(x_2\cdot u_1)u_1+v_2=(x_2\cdot u_1)u_1+(x_2\cdot u_2)u_2\\ x_3&=(x_3\cdot u_1)u_1+(x_3\cdot u_2)u_2+v_3\\ &=(x_3\cdot u_1)u_1+(x_3\cdot u_2)u_2+(x_3\cdot u_3)u_3 \end{aligned}\]따라서 위 식을 행렬로 표현하면 다음과 같습니다.
\[\begin{aligned} \begin{bmatrix} x_1\quad x_2\quad x_3 \end{bmatrix} &= \begin{bmatrix} (x_1\cdot u_1)u_1\quad (x_2\cdot u_1)u_1+(x_2\cdot u_2)u_2\quad (x_3\cdot u_1)u_1+(x_3\cdot u_2)u_2+(x_3\cdot u_3)u_3 \end{bmatrix} \\ &=\begin{bmatrix} u_1\quad u_2\quad u_3 \end{bmatrix} \begin{bmatrix}x_1\cdot u_1&x_2\cdot u_1&x_3\cdot u_1 \\0&x_2\cdot u_2&x_3\cdot u_2\\0&0&x_3\cdot u_3 \end{bmatrix} \\ \implies A&=QR \end{aligned}\]이렇게 하여 행렬 $A$를 Orthogonal Matrix인 $Q$와 Upper Triangular Matrix인 $R$의 곱으로 분해할 수 있게 됩니다. (참고로 $Q$의 열들은 Orthonormal 벡터이지만, 이 행렬 자체는 Orthonormal Matrix가 아닌 Orthogonal Matrix 로 부른다고 합니다.) 한편, 상삼각 행렬인 $R$에 주목해봅시다. 위 정리에 의하면 $R$은 역행렬이 존재(invertible)한다는데 왜 그런지 확인해보겠습니다! $R$이 invertible하기 위해서는 대각 요소들이 모두 0이 아니어야 할 것입니다. 위에서 Orthonormal 벡터 $u_1, u_2, u_3$으로 원래 벡터 $x_1,x_2,x_3$을 재구성한 식들을 참고했을 때, 행렬 $R$의 대각 요소 에 해당하는 $(x_1\cdot u_1), (x_2\cdot u_2), (x_3\cdot u_3)$은 각각 Orthogonal 벡터 $v_1,v_2,v_3$의 길이 에 해당합니다. 벡터 $v_1$의 길이가 $x_1\cdot u_1$과 어떻게 같은지에 대해서는 아래 식을 참고해주세요! Orthonormal 벡터의 길이가 1이라는 것, 즉 $u_1\cdot u_1=1$을 이용하면 다음과 같습니다.
한편, $R$은 Orthogonal Matrix $Q$가 $Q^{\intercal}Q=I$인 것을 이용하여 다음과 같이 쉽게 구할 수 있습니다.
\[\begin{aligned} A&=QR\\Q^{\intercal}A&=Q^{\intercal}QR=R\\ \therefore R&=Q^{\intercal}A \end{aligned}\]잘 이해되셨나요? 여기까지 Gram-Schmidt Process 와 QR Decomposition 에 대한 기록이었습니다! 다음 포스트에서는 Least Squares Solution에 대해서 정리하고자 합니다. 감사합니다 :)
$Reference.$
- David C.Lay · Stephen R.Lay · Judi J.McDonald, Linear Algebra and its Applications, 5th edition, Pearson
- 고려대학교 김홍중 교수님의 수업