[선형대수] Orthogonal Projection
안녕하세요! 이번 포스트에서는 정사영(Orthogonal Projection) 에 대해 제가 배웠던 내용을 정리하고자 합니다. 바로 시작하겠습니다 😊
1. 정사영(Orthogonal Projection)의 정의
다음 그림처럼 2차원 평면에 어떠한 벡터 $y$가 있다고 합시다. 이 $y$를 2개의 서로 다른 벡터의 합으로 쪼개려고 하는데요. 하나는 벡터 $u$ 위에 있는 벡터로, 즉 $αu$로 하고, 또 다른 벡터는 $u$와 직교인 벡터로 하고자 합니다. 이제 전자는 $\hat y$으로, 후자는 $z$로 표기할게요. 이때, $z$는 $u$와 직교하기 때문에 $z\cdot u=0$이 됩니다. 이걸 이용해서 정리하면 $αu$에서의 $α$가 무엇이어야 하는지 다음과 같이 도출됩니다!

이 때의 $\hat y=\frac {y\cdot u}{u\cdot u} u$를 벡터 $y$의 $u$에 대한 정사영(orthogonal projection of $y$ onto $u$)라고 하고, $z=y-\hat y$를 $u$에 수직인 $y$의 벡터성분(component of $y$ orthogonal to $u$)라고 합니다! 이 때 $u$에 어떠한 스칼라 $c$를 곱해도, Orthogonal Projection of $y$ onto $cu$ 와 Orthogonal Projection of $y$ onto $u$ 는 같습니다! 따라서, 이를 더욱 일반화해서 $u$라는 벡터에 의해 생성되는 어떠한 부분공간 $W$에 대한 벡터 $y$의 정사영(orthogonal projection of $y$ onto $W$)이라고 일컫습니다.
\[\hat y=\frac {y\cdot u}{u\cdot u} u=proj_{\scriptsize W} y,\quad W=span\{ u \}\]위 그림과 같이, 정사영이라는 것은 어떤 부분공간에 존재하는 벡터를 (일반적으로) 그 부분공간보다 낮은 차원의 부분공간으로 투영시키는 것이라고 할 수 있습니다. 제가 땅에 서 있을 때 저의 그림자는, 2차원인 땅에 3차원인 제가 투영된 것이라고 할 수 있을 것입니다. 이것의 의미에 대해서는 후에 Least Squares Solution에 대해 포스팅할 때 조금 더 구체적으로 정리하고자 합니다.
2. 기하학적 의미
그런데 위 식에서 $u$의 가중치 $\frac {y\cdot u}{u\cdot u} $ 어디서 많이 보지 않았나요?
저번 글에서 y는 특정한 가중치들을 가진 직교 기저들의 선형결합으로 표현가능하다 는 정리를 배웠었는데요. 예를 들어서, {$u_1,u_2 $}가 $\mathbb{R}^2$의 직교기저라고 해봅시다. 그러면 정리에 의해, $\mathbb{R}^2$의 모든 벡터 $y$는 다음과 같이 표현 가능하다는 정리였습니다.
그런데 앞서, $\frac{y\cdot u_1}{u_1\cdot u_1} u_1$은 $u_1$에 대한 $y$의 정사영이고, $\frac {y\cdot u_2}{u_2\cdot u_2} u_2$는 $u_2$에 대한 $y$의 정사영이라는 걸 배웠기 때문에 위 식은 다음과 같이 나타낼 수 있게 됩니다!
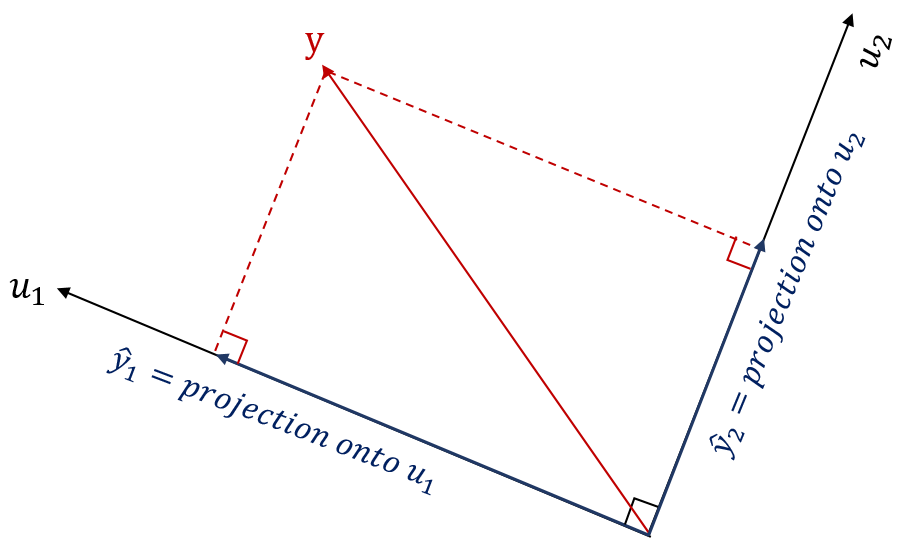
\[y=proj_{span\{ u_1\}}y+proj_{span\{ u_2\}} y\]즉, $\mathbb{R}^2$의 모든 벡터는, $\mathbb{R}^2$의 직교 기저에 해당하는 벡터들 $(eg.\space u_1,u_2)$ 각각에 대한 정사영의 합으로 표현할 수 있습니다. 이걸 그림으로 나타내면 다음과 같습니다!
3. Orthogonal Decomposition Theorem
다시 돌아와서, 1번에서 했던 쪼개기 과정을 다시 주목해봅시다! 이 과정을 일반화하는 정리가 있는데요. 바로 Orthogonal Decomposition Theorem 이라 일컫습니다.
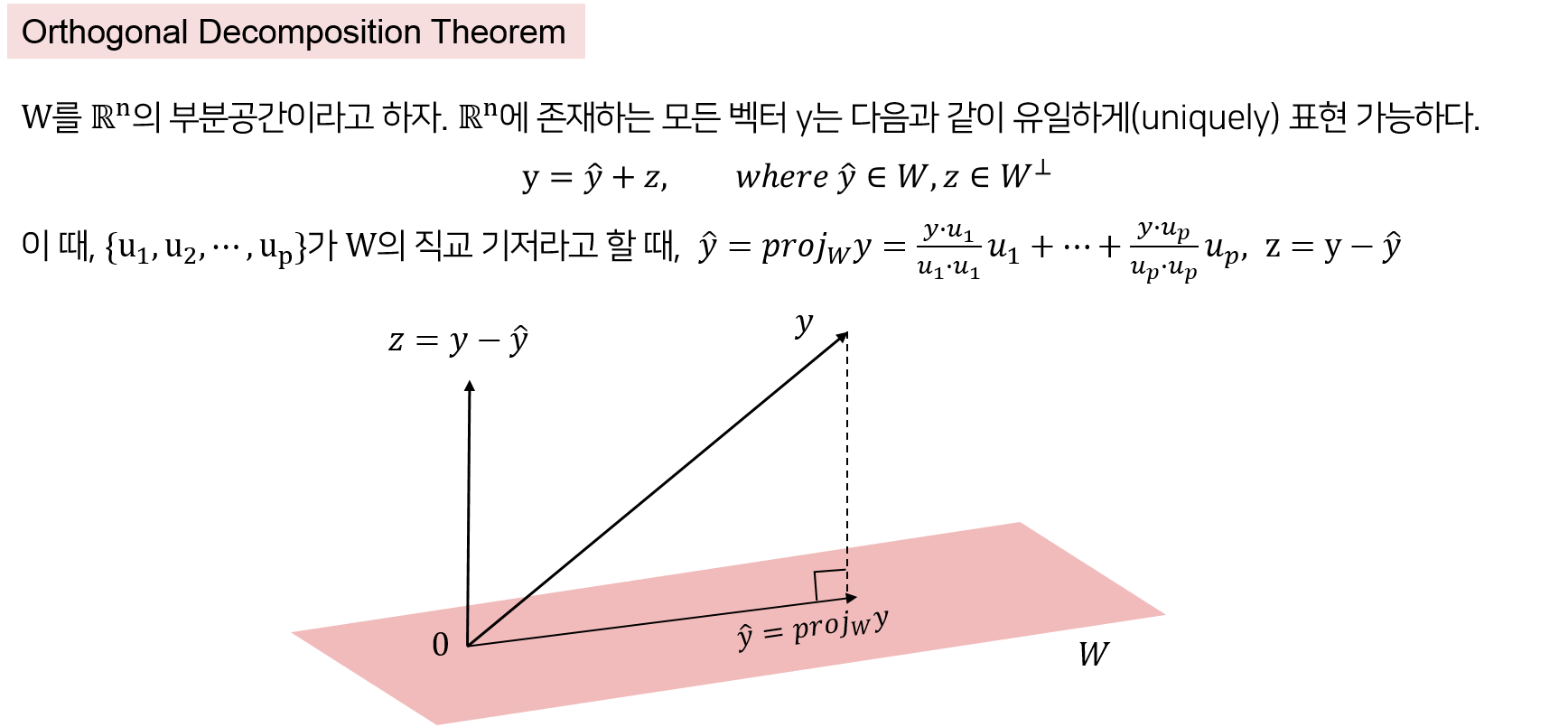
위 정리에 의하면, $\mathbb{R^n}$에 존재하는 벡터 $y$는 이를 부분공간 $W$에 정사영시킨 벡터 와 $W$에 수직인 벡터 의 합으로 유일하게 분해됩니다! 근데 여기서 주목할 것은 어떻게 저 분해가 유일하냐는 건데요. 이를 한번 간단하게 증명해보겠습니다. Orthogonal decomposition이 유일하지 않다고 가정했을 때, 이 가정에 오류가 생기는 것을 보이는 논리입니다.
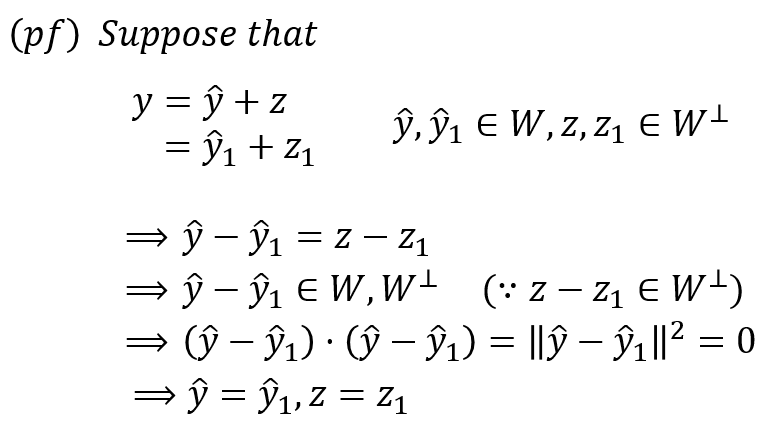
4. Projection Matrix
이번에는 {$u_1,u_2,\cdots, u_p$}이 직정기저(Orthonormal basis) 라고 해볼까요? 그러면 3번에서 했던 Orthogonal Decomposition Theorem 에서 벡터 $y$의 $W$로의 정사영은 다음과 같이 표현될 것입니다.
이 식을 내적의 성질을 이용하면 다음과 같습니다.
\[\begin{aligned} proj_{\scriptsize W} y&=(u_1\cdot y)u_1+(u_2\cdot y)u_2+\cdots+(u_p\cdot y)u_p\\ &=(u_1^T y)u_1+(u_2^T y)u_2+\cdots+(u_p^T y)u_p\\ &=𝑢_1 (𝑢_1^T 𝑦) +𝑢_2 (𝑢_2^T 𝑦) +⋯+𝑢_𝑝 (𝑢_𝑝^T 𝑦)\\ &=(𝑢_1 𝑢_1^T) 𝑦 +(𝑢_2 𝑢_2^T) 𝑦 +⋯+(𝑢_𝑝 𝑢_𝑝^T )𝑦\\ &=(u_1u_1^T+𝑢_2 𝑢_2^T+\cdots+𝑢_𝑝 𝑢_𝑝^T )y\\ &=\begin{bmatrix} u_1&u_2&\cdots&u_p\end{bmatrix} \begin{bmatrix}u_1^T\\u_2^T\\ \vdots\\u_p^T\end{bmatrix}y\\ &=UU^Ty, \quad if\space U=\begin{bmatrix} u_1&u_2&\cdots&u_p\end{bmatrix} \end{aligned}\]위 식에서, 벡터 $y$에 $UU^T$라는 nxn 행렬을 곱한 것이 벡터 $y$의 $W$로의 정사영(Projection of $y$ onto $W$)이 되었습니다. 즉, 벡터 $y$는 $UU^T$ 행렬에 의해 선형변환된 것입니다.
$Proj_{\scriptsize W} y$ is an image of $y$ transformed by $UU^T$
따라서, 이 행렬 $UU^T$을 $\small Transformation\space Matrix$라고 하고, 변환시키는 것 중에서도 정사영시키는 역할을 하기 때문에 $\small Projection\space Matrix$라고 일컫습니다.
잘 이해되셨나요? 이제 정리해보겠습니다. $\mathbb{R^n}$의 부분공간 $W(\not=\mathbb R^n)$가 있다고 합시다. $\mathbb{R^n}$의 직정기저(orthonormal basis)가 $\lbrace u_1,u_2, \cdots, u_n\rbrace $이라 하고, $W$의 직정기저가 $\lbrace u_1, u_2, \cdots, u_p \rbrace,\space (p<n)$라고 할 때, 먼저 $\mathbb{R^n}$의 모든 벡터 $y$는 다음과 같이 표현가능합니다.
\[y=(u_1\cdot y)u_1+(u_2\cdot y)u_2+\cdots+(u_n\cdot y)u_n\]한편, 부분공간 $W$에 대한 벡터 $y$의 정사영$(\hat y)$은 다음과 같이 표현됩니다.
\[\hat y=(u_1\cdot y)u_1+(u_2\cdot y)u_2+\cdots+(u_p\cdot y)u_p\]Orthogonal Decomposition Theorem 에 의해, $y$는 다음과 같이 쪼개집니다.
\[y=\hat y + z, \quad z=y-\hat y\]이 때, $z$는 $y$에서 $\hat y$를 뺀 부분이며, $W$에 직교하는 벡터입니다.
\[z=(u_{p+1}\cdot y)u_{p+1}+\cdots+(u_n\cdot y)u_n\space \perp\space W\]여기까지 Orthogonal Projection 에 대한 기록이었습니다! 다음 포스트에서는 Gram-Schmidt Process와 QR 분해에 대해서 정리하고자 합니다. 감사합니다 :)
$Reference.$
- David C.Lay · Stephen R.Lay · Judi J.McDonald, Linear Algebra and its Applications, 5th edition, Pearson
- 고려대학교 김홍중 교수님의 수업