[이산형 분포] 초기하 분포(Hypergeometric distribution)
이번 포스트에서는 초기하분포(Hypergeometric Distribution) 에 대해 알아보고, 기대값과 분산을 구하며, 이항분포와의 관계에 대해서 정리하고자 합니다.
초기하 분포(Hypergeometric Distribution)
파란공과 빨간공이 5개씩 들어있는 주머니에서 5개의 공을 비복원으로 뽑고, 뽑은 공 중에서 2개는 파란 공, 3개는 빨간 공일 확률을 구하는 문제를 생각해봅시다. 중고등학교 때 확률 단원 배울 때마다 나왔던 문제인 것 같은데요. 저는 대학 가서도 이런 문제를 풀고있을 줄은 몰랐습니다,,ㅎㅎ 아무튼 바로 이 문제가 초기하분포 그 자체입니다! N개의 구성원으로 이루어진 어떤 모집단이 존재하고, 이 모집단이 두 그룹으로 나누어진다고 합시다. 첫번째 그룹에는 M개의 구성원이 있다고 하면, 다른 그룹에는 N-M개의 구성원이 존재할 것입니다. 이 때, 초기하 확률변수 X는 전체 모집단에서 K개의 샘플을 비복원으로 뽑을 때, K개 샘플 중에서 첫번째 그룹에 해당하는 샘플 수를 의미합니다.
\[\begin{gathered} X\sim Hypergeometric(N, M, K) \cr f_X(x) =\frac{\binom{M}{x} \binom{N-M}{K-x}}{\binom{N}{K}}, \cr ( x=max\lbrace 0, M-N+K\rbrace, \cdots , min\lbrace K,M\rbrace )\end{gathered}\]다시 강조하면 초기하분포에서는 샘플을 비복원추출하는 것입니다. 그런데 위와 똑같은 상황에서 샘플을 복원추출하면 뭐가 되나요? 바로 저번 포스트에서 정리했던 이항분포 에 해당합니다! 똑같은 상황에서 샘플을 복원추출하는 개념은 이항분포, 비복원추출하는 개념은 초기하분포라고 정리할 수 있을 것입니다.
평균과 분산, 그리고 이항분포와의 비교
그러면 이제 초기하분포의 평균을 구해봅시다.
\[\begin{aligned} E(X) &= \sum_{x=0}^K x\frac{\binom{M}{x} \binom{N-M}{K-x}}{\binom{N}{K}} \cr &= \frac{M}{\frac{N}{K}} \cdot \sum_{x=1}^K \frac{\binom{M-1}{x-1} \binom{N-M}{K-x}}{\binom{N-1}{K-1}} \cr &= K\frac{M}{N}\cdot \sum_{z=0}^{K-1} \frac{\binom{M-1}{z} \binom{N-1-M+1}{K-1-z}}{\binom{N-1}{K-1}} , \space ( z=x-1) \cr &= K\frac{M}{N} \end{aligned}\]이 때, 초기하 분포의 평균이 이항분포 의 평균과 매우 유사하다는 것을 알 수 있습니다! 이항분포 포스트에서 했듯이 $\small Binomial(n, p)$를 따르는 확률변수의 평균은 $\small np$인데요. 초기하분포에서도 $\small K$는 표본의 크기, $\frac {M}{N}$은 전체 모집단 대 관심 있는 그룹의 비, 즉 관심 있는 그룹이 뽑힐 확률이므로 성공 확률 에 해당합니다! 이번에는 초기하분포의 분산을 구해보겠습니다.
\[\begin{aligned} E(X(X-1)) &= \sum_{x=0}^K x(x-1)\frac{\binom{M}{x} \binom{N-M}{K-x}}{\binom{N}{K}} \cr &= \frac{M(M-1)}{\frac{N(N-1)}{K(K-1)}} \cdot \sum_{x=2}^K \frac{\binom{M-2}{x-2} \binom{N-M}{K-x}}{\binom{N-2}{K-2}}\cr &= K(K-1)\frac{M(M-1)}{N(N-1)} \cr \end{aligned}\] \[\begin{aligned}Var(X) &= E(X(X-1)) + E(X) - [E(X)]^2\cr &= K \frac{M}{N} \frac{N-M}{N}\cdot \frac{N-K}{N-1} \end{aligned}\]위와 같이 분산을 구한 결과, 앞의 세 항 $ K\frac{M}{N} \frac{N-M}{N}$ 역시 이항 분포의 분산과 매우 비슷합니다! 이항분포에서의 분산이 $\small np(1-p)$였던 것을 고려할 때, 초기하분포에서는 $\small K$가 표본의 크기, $\small \frac {M}{N}$은 성공 확률, $\small \frac {N-M}{N}$은 실패 확률에 해당합니다!
그런데 초기하분포의 분산에는 뒤에 한가지 항 $\small \frac{N-K}{N-1}$이 더 붙은 것을 확인할 수 있는데요. 이 항을 바로 유한모집단수정항(finite population correction term)이라고 일컫습니다! 이름 그대로, 초기하분포는 비복원추출을 하기 때문에 모집단이 유한집단이 되고, 이로 인해 나타나는 항입니다. $\small K$는 대체로 1보다 크기 때문에 이 항은 1보다 작게 되고, 그에 따라 초기하분포는 이항분포의 분산보다 작다고 합니다.
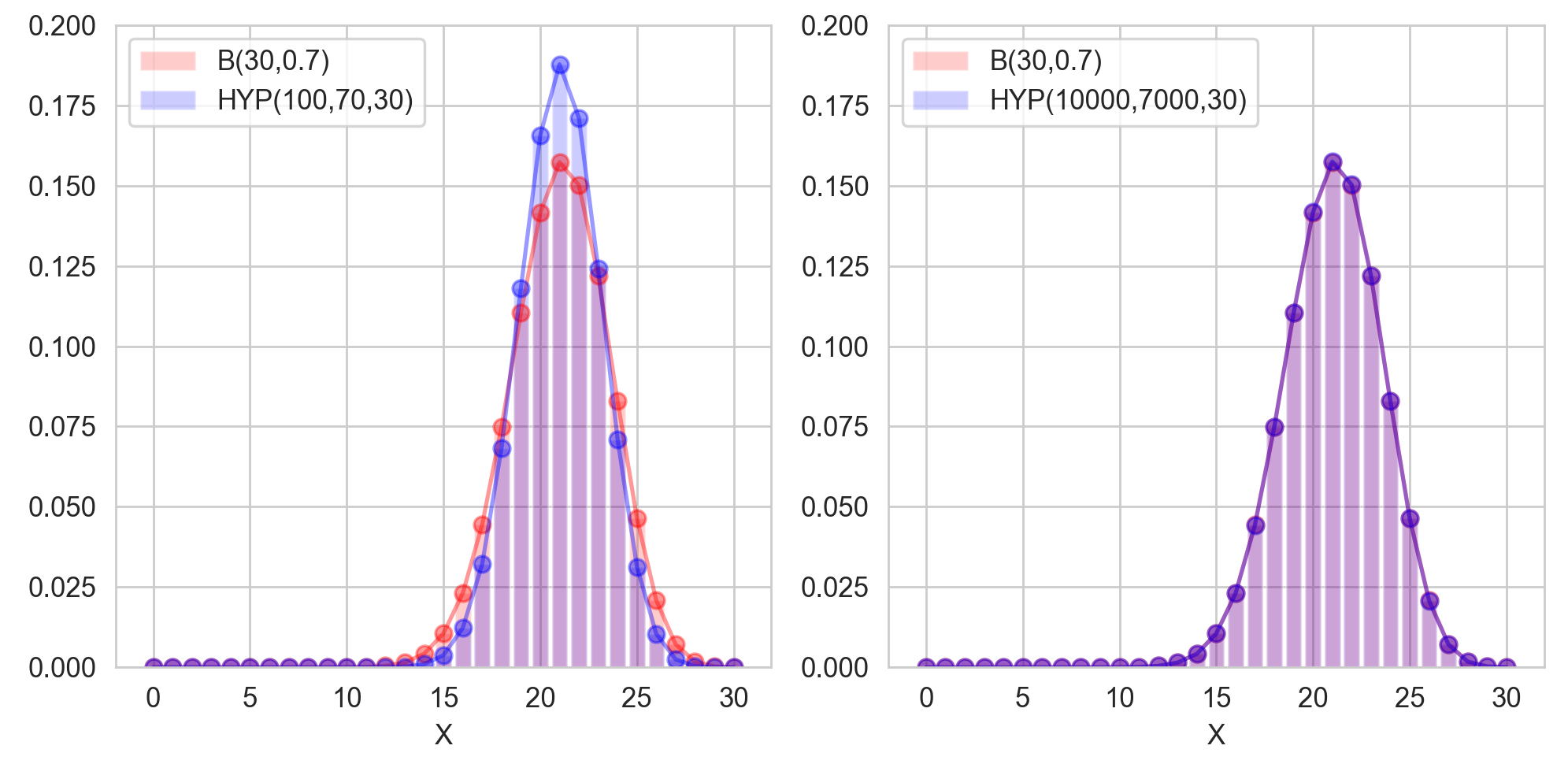
한편, 모집단의 크기 $N$이 무한대에 가까워지게 커지면, 유한모집단수정항은 1에 가까워질 것입니다. 이 경우에는 이항 분포의 분산에 근사하게 될 것입니다. 직관적으로 모집단의 크기가 무한대로 가까워지면, 아무리 비복원추출이라도 유한집합이 아니게 되고, 복원추출이나 다를바 없게 될 것입니다. 실제로, $\small X\sim Hypergeometric(N, M, n)$이라 할 때, 모집단의 크기 $N$과 첫번째 그룹의 크기 $M$이 무한대로 가고, $\frac{M}{N}$이 $p$에 수렴할 때, 초기하분포는 이항분포에 근사하게 됩니다.
\[\lim_{N\rightarrow \infty}\frac{\binom{M}{x} \binom{N-M}{n-x}}{\binom{N}{n}} = \binom{n}{x}p^x(1-p)^{n-x}\]마지막으로 초기하분포가 이항분포에 근사하는 것을 증명하고 마치겠습니다!
\[\small\begin{aligned} \frac{\binom{M}{x} \binom{N-M}{n-x}}{\binom{N}{n}} &= \frac{M!}{x! (M-x)!}\cdot \frac{(N-M)!}{(n-x)!(N-M-(n-x))!}\cdot \frac{n!(N-n)!}{N!}\cr &= \binom{n}{x}\cdot \frac{M! / (M-x)!}{N!/(N-x)!}\cdot \frac{(N-m)!(N-n)!}{(N-x)!(N-m-(n-x))!} \cr &= \binom{n}{x}\cdot \frac{M! / (M-x)!}{N!/(N-x)!}\cdot \frac{(N-M)!/(N-M-(n-x))!}{(N-n+(n-x))!/(N-n)!}\cr &=\binom{n}{x}\prod_{i=1}^x{\frac{M-x+i}{N-x+i}}\cdot \prod_{k=1}^{n-x}{\frac{N-M-(n-x)+k}{N-n+k}} \cr &\rightarrow \binom{n}{x}p^x(1-p)^{n-x} \space as \space N,M\rightarrow \infty, \frac{M}{N}\rightarrow p\end{aligned}\]$Reference$