[이산형 분포] 포아송 분포(Poisson distribution)

About Mathematical Statistics

이번 포스트에서는 포아송분포(Poisson Distribution) 에 대해 알아보고, 이것의 기대값, 분산, 적률생성함수를 구해보겠습니다. 나아가 포아송분포와 이항분포와의 관계에 대해서도 알아보겠습니다.

포아송 분포(Poisson Distribution)

우리나라에서 1년동안 일어나는 비행기 사고 횟수, 특정 시간동안 어떤 주유소에 도착하는 차량의 개수 등 어떤 단위 구간(시간)에서 일어나는 특정 사건의 발생 횟수 분포에 관한 것이 바로 포아송 분포 입니다. 즉, 포아송 분포를 통해서 평균 발생 횟수가 5개 되는 단위 구간에서 사건이 3개 일어날 확률은 어느정도 되는지 구할 수 있습니다. 한편, 특정 시간 또는 구간에서 평균 발생 횟수는 알 수 있지만, 그 구간 내 각 사건은 랜덤으로 일어나서 정확한 타이밍은 예측할 수 없습니다. 그 구간 내 사건이 랜덤으로 발생하지 않고, 어떠한 규칙에 의해 발생한다면 포아송 분포라고 할 수 없을 것입니다. 이 뿐만 아니라, 포아송 분포를 따른다고 말할 수 있으려면 사건의 발생횟수는 다음의 성질들을 만족해야 합니다.

  • 서로 겹치지 않는 단위 구간에서 발생한 사건들은 서로 독립이다.
  • 단위 구간의 크기 대비 사건의 평균 발생 횟수의 비율은 일정하다.
  • 같은 사건이 거의 동시에 일어날 확률은 0이다.

어떤 사건이 위의 세가지 성질을 만족하면서 일어나면 이 사건은 포아송 확률과정 을 따른다고 말합니다. 포아송 확률과정을 따르는 사건이 단위 구간에서 발생하는 횟수는 포아송 분포를 따르게 됩니다. 평균 발생 횟수가 $\lambda$인 포아송 확률변수의 확률밀도함수는 다음과 같습니다.

\[f_X(x) = \frac{e^{-\lambda}\lambda^x}{x!}, \space x= 0,1,2,\cdots\]

이제 포아송 분포의 기대값, 분산, 적률생성함수를 구하면 다음과 같습니다.

\[\begin{aligned} E(X) &= \sum_{x=0}^\infty x\cdot \frac{e^{-\lambda}\lambda^x}{x!} \cr &= \lambda \sum_{x=1}^\infty \frac{e^{-\lambda}\lambda^{x-1}}{(x-1)!} \cr &= \lambda \cr E(X(X-1)) &= \sum_{x=0}^\infty x(x-1)\frac{e^{-\lambda}\lambda^x}{x!} \cr &= \lambda^2 \sum_{x=2}^\infty \frac{e^{-\lambda}\lambda^{x-2}}{(x-2)!} \cr &= \lambda^2 \cr Var(X) &= E(X(X-1)) + E(X) -[E(X)]^2 \cr &= \lambda^2 +\lambda -\lambda^2 \cr &= \lambda \cr M_X(x) &= E(e^{tX}) = \sum_{x=0}^\infty e^{tx}\cdot \frac{e^{-\lambda}\lambda^x}{x!}\cr &= e^{-\lambda}\sum_{x=0}^\infty \frac{(\lambda e^t)^x}{x!} \cr &= e^{-\lambda}\cdot e^{\lambda e^t} \cr &= e^{\lambda (1-e^t)} \end{aligned}\]

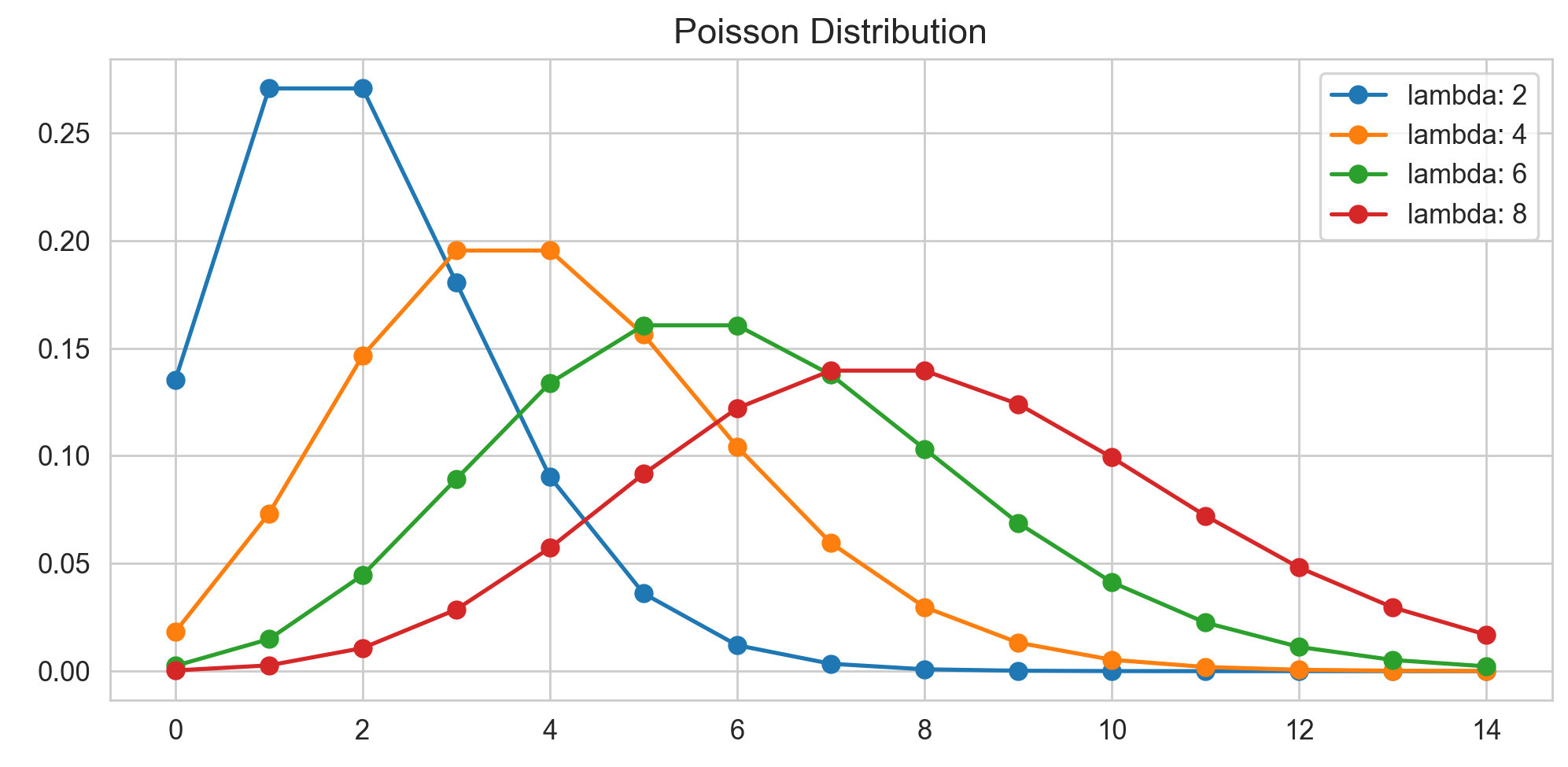
여기서 눈여겨볼 점은 포아송 분포는 기대값과 분산이 서로 같다는 것입니다. 아래 그림의 각 람다에 따른 포아송 분포를 보면, 람다에서 확률값이 거의 가장 큰 것을 확인할 수 있습니다. 람다가 기대값이므로, 람다에서 확률값이 제일 높은 건 어느정도 자명해보입니다. 또 한, 분산 역시 람다이므로, 람다가 커질수록 분산도 커져서 분포가 넓게 퍼지게 되는 것을 확인할 수 있습니다.


이항분포의 포아송 분포로의 근사

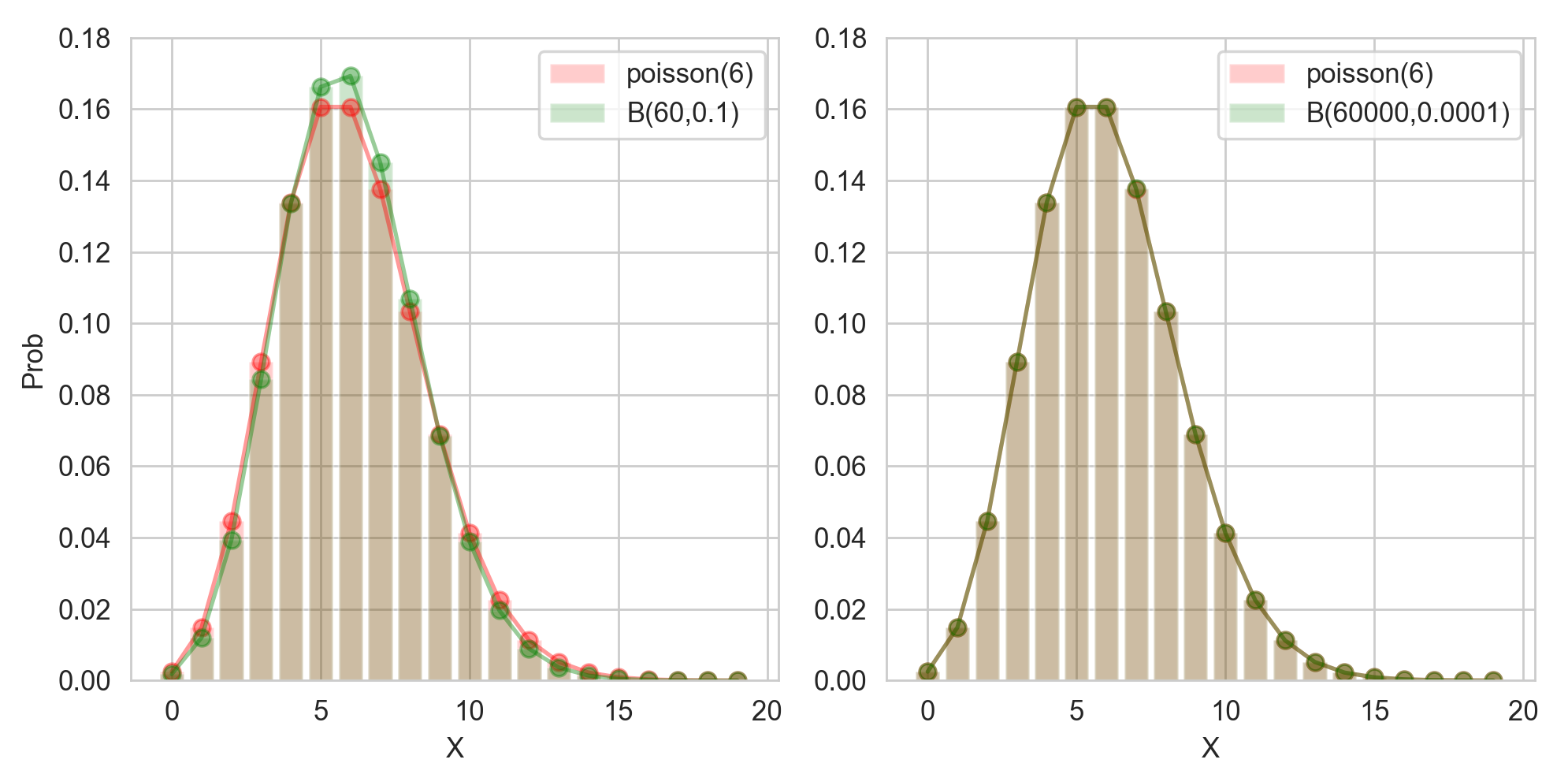
한편, 저번 포스트에서 했던 이항 분포는 특정 조건 하에서 포아송 분포로 근사하게 됩니다.

\[\begin{gathered}\binom{n}{x} p^x(1-p)^{n-x} \longrightarrow \frac{e^{-\lambda}\lambda^x}{x!} \cr as \space n\rightarrow \infty ,\space p\rightarrow 0,\space np\rightarrow \lambda \end{gathered}\]

이걸 수리적으로 증명해보겠습니다. $p=\frac{\lambda}{n} + o(\frac{1}{n})$에서 $n$은 무한대로 커지므로, $p=\frac{\lambda}{n}$으로 두고 풀겠습니다!

\[\begin{aligned} \binom{n}{x}p^x(1-p)^{n-x} &= \frac{n!}{x!(n-x)!} \bigg (\frac{\lambda}{n}\bigg )^x \bigg ( 1-\frac{\lambda}{n} \bigg )^{n-x} \cr &= \frac{\lambda^x}{x!}\cdot \bigg (1-\frac{\lambda}{n} \bigg )^n\cdot \frac{n!}{(n-x)!(n-\lambda)^x} \cr &= \frac{\lambda^x}{x!}\cdot \bigg (1-\frac{\lambda}{n} \bigg )^n\cdot \frac{n(n-1)\cdots (n-x+1)}{(n-\lambda)^x} \cr &\longrightarrow \frac{\lambda^x}{x!}\cdot e^{-\lambda} \cdot 1 \end{aligned}\]

이항분포는 계산해보면 $n$이 조금만 커져도 계산하는 과정이 정말 복잡해집니다. 이 대신, 시행 횟수가 매우 클 경우, 성공 확률은 낮다면 이것의 평균을 이용해서 포아송 분포를 이용하면 되는 것입니다. 즉, 포아송 분포는 시행횟수가 측정이 불가할 정도로 클 경우에, 평균 성공 횟수만 알면 이용할 수 있는 것입니다. 예를 들어, 1년 동안 특정 고속도로 구간을 통과하는 차량의 개수는 측정하기가 쉽지 않을 정도로 매우 많을 것입니다. 그러나, 그 고속도로 구간에서 사고가 날 확률은 낮을 것입니다. 이 경우, 1년동안 해당 고속도로에서 일어나는 평균 사고 횟수를 포아송 분포로 쉽게 구할 수 있게 됩니다.


$Reference$