[이산형 분포] 기하 분포(Geometric distribution)
이번 포스트에서는 기하분포(Geometric Distribution)에 대해 알아보고, 기대값과 분산, 적률생성함수까지 구해보고자 합니다.
기하 분포(Geometric Distribution)
주사위를 숫자 1이 나올때까지 돌린다고 해봅시다. 바로 1이 나올 수도 있고, 한참을 돌려야 1이 나올 수도 있을 것입니다. 이 때 각 주사위 숫자가 나올 확률은 매 시행에서 같을 것이고, 각 시행은 서로에게 어떠한 영향을 주지 않을 것입니다. 이 시행을 뭐라고 하나요? 바로 베르누이 포스트에서 다뤘던 베르누이 시행입니다! 베르누이 시행을 독립적으로 반복해서 성공을 얻을 때까지 걸리는 시행 횟수, 이것과 관련한 분포가 바로 기하분포입니다!
어떤 확률변수 X가 ‘성공(success)’ 확률이 p인 시행을 반복하여 처음으로 ‘성공’이 나타난 시도 횟수, 다시 말해서 처음으로 ‘성공’을 얻기 위해 걸렸던 시행 횟수라고 할 때, 이 X는 성공확률이 p인 기하분포를 따른다고 말합니다.
\[\begin{gathered} X \sim Geometric(p) \cr f_X(x) = (1-p)^{x-1}p,\space x=1,2,\cdots \end{gathered}\]아래 그림은 각 성공 확률에 따른 기하 분포입니다. 성공 확률이 클 수록 초반에 ‘성공’이 나타날 확률이 크고, 성공 확률이 작을수록 초반에 ‘성공’이 나타날 확률이 작은 것을 확인할 수 있습니다.
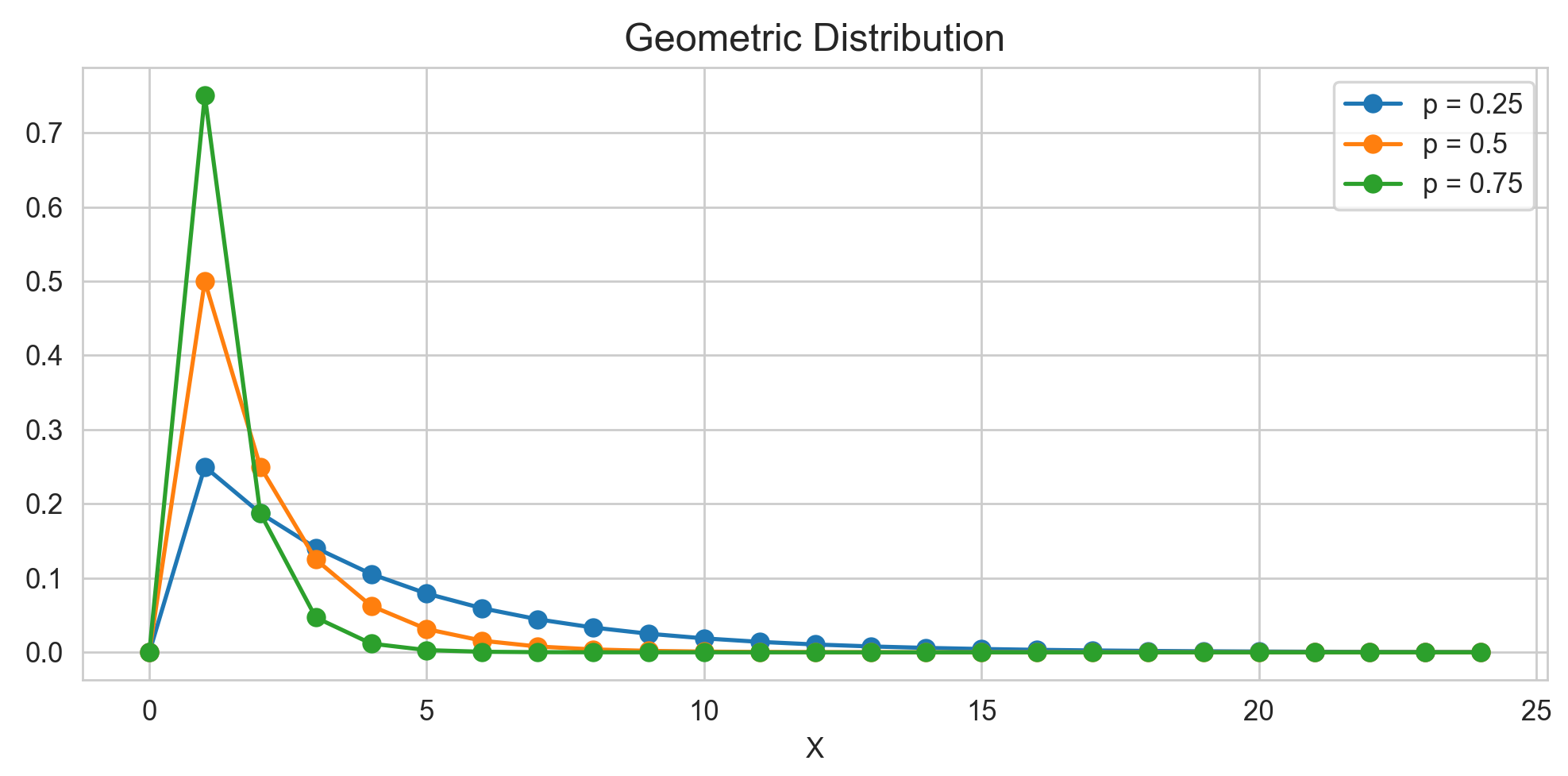
기하분포의 기대값, 분산, 적률생성함수
이제 기하분포의 기대값과 분산, 적률생성함수를 구해봅시다. 먼저 기대값입니다.
어떻게 구하면 될까요? 일단 기하분포의 전체 확률 값이 1이 되는 것을 이용해서 다음과 같이 정리해보겠습니다.
\[\sum_{x=1}^\infty (1-p)^{x-1}p = 1 \implies\sum_{x=1}^\infty (1-p)^x = \frac{1-p}{p}\]이제 양변을 p로 미분해보겠습니다. 그러면 다음과 같이 기대값을 구하기 위해 필요한 식을 얻을 수 있습니다.
\[\begin{aligned} \frac{d}{dp}\sum_{x=1}^\infty (1-p)^x &=\sum_{x=1}^\infty \frac{d}{dp} (1-p)^x = \sum_{x=1}^\infty x(1-p)^{x-1}\cdot (-1) \cr &= -\frac{1}{p^2} = \frac{d}{dp}\frac{1-p}{p} \cr &\therefore \sum_{x=1}^\infty x(1-p)^{x-1} =\frac{1}{p^2} \end{aligned}\]따라서 기하분포의 기대값은 다음과 같이 될 것입니다.
\[E(X)= \sum_{x=1}^\infty x(1-p)^{x-1}p=\frac{1}{p^2}\cdot p = \frac{1}{p}\]
이번엔 분산을 구해보겠습니다. 분산을 구하기 전에 먼저 위에서 미분을 통해 구했던 것을 한번 더 미분하겠습니다.
그렇다면 위 식을 이용해서 $E(X(X-1))$을 먼저 구할 수 있을 것입니다.
\[\small E(X(X-1))=\sum_{x=1}^\infty x(x-1)(1-p)^{x-1}p=(1-p)p\cdot \frac{2}{p^3}\]따라서 다음과 같이 분산을 구할 수 있게 됩니다.
\[\begin{aligned} Var(X)&=E(X(X-1))+E(X) - (E(X))^2\cr &= \frac{2(1-p)}{p^2}+\frac{1}{p}-\frac{1}{p^2}=\frac{1-p}{p^2}\end{aligned}\]
마지막으로 적률생성함수를 구해보겠습니다.
기하분포의 무기억성(Memoryless Property)
한편, 기하 분포는 무기억성이라는 성질을 갖고 있습니다. 어떤 성공 사건이 일어나고 그 다음 사건이 다시 일어날 때까지 시행을 반복한다고 합시다. 현재까지 $k$번 만큼 시행을 했는데, 아직도 성공 사건이 안 일어났습니다. 이 때, ‘무기억성’이라는 것은, 사건이 일어나기까지 남은 시행은 $k$번 만큼 기다린 것과 전혀 상관 없이 처음부터 기다린 것과 같다는 것입니다! 천 번을 주사위를 돌렸는데 1이 안 나왔다 해도, 처음부터 돌린 것보다 1이 나올 확률이 더 높다거나 이런건 아니라는 거죠! 이걸 식으로 쓰면 다음과 같습니다.
\[P(X=x+k \vert X>k) = P(X=x)\]이걸 증명해보겠습니다.
\[\begin{aligned} P(X=x+k) &= (1-p)^{x+k-1}p \cr P(X>k) &= \sum_{x=k+1}^\infty (1-p)^{x-1}p \cr &= \frac{p}{1-p} \sum_{x=k+1}^\infty (1-p)^x \cr &= (1-p)^{k} \cr P(X=x+k \vert X>k) &= \frac{P(X=x+k)}{P(X>k)} \cr &= \frac{(1-p)^{x+k-1}p}{(1-p)^{k}} \cr &= (1-p)^{x-1}p\cr &= P(X=x), \space x=1,2,\cdots \end{aligned}\]무기억성에 대해서는 다음에 연속형 분수인 지수분포에 대해서 포스팅할 때 한번 더 등장할 예정입니다!
여기까지 기하분포의 이모저모에 대해 알아보았는데요. 그런데 이제 주사위 1이 나오는 걸 한번 얻을 때까지 걸리는 시행횟수 말고, 총 5번 얻을 때까지의 시행횟수가 궁금한 경우도 있을 것입니다. 즉, 기하분포를 더 확장할 수 있을 것 같은데요. 이렇게 성공의 횟수 1개로 국한하지 않을 때가 바로 음이항분포이고, 이에 대해서 다음 포스트에서 정리하고자 합니다.
$Reference$
- 송성주, 전명식. (2015). 수리통계학
- 고려대학교 송성주 교수님의 수업
){kind=link}