[이산형 분포] 음이항 분포(Negative Binomial distribution)
이번 포스트에서는 기하분포(Geometric Distribution)를 확장한 음이항분포(Negative Binomial Distribution) 에 대해 알아보겠습니다. 기대값과 분산, 적률생성함수를 구하고, 음이항분포와 이항분포와의 관계, 음이항분포와 포아송분포와의 관계에 대해서도 정리하고자 합니다.
음이항 분포(Negative Binomial Distribution)
기하분포와 똑같은 조건에서 어떤 확률 변수 $X$를 $r$번째 성공을 얻을 때까지 걸리는 시행횟수라고 해봅시다. 이때의 $X$를 음이항 확률변수라고 하고, 분포를 음이항분포라고 합니다. $(i.e. \space X\sim Negative\space Binomial(r,p))$ 즉, $r=1$인 경우가 바로 기하분포인거죠? 따라서 음이항분포는 기하분포를 일반화한 것이라고 할 수 있습니다.
\[f_X(x) = \binom{x-1}{r-1}p^r (1-p)^{x-r},\space x=r, r+1, \cdots\]따라서 기대값과 분산도 기하분포를 이용하면 매우 쉽게 구할 수 있게 됩니다. 기하분포의 기대값과 분산은 저번 포스트를 참고해주세요!
\[X_1, \cdots, X_r \overset{iid}{\sim} GEO(p) \implies X=X_1+\cdots+X_r \sim NB(r,p)\] \[\begin{aligned} E(X)&=E(X_1)+\cdots +E(X_r)= r\cdot \frac{1}{p}\cr Var(X)&= Var(X_1)+\cdots +Var(X_r)=r\cdot \frac{1-p}{p^2} \end{aligned}\]한편, 음이항 분포는 ‘음’이항분포라는 이름을 가지고 있는데요. 이름에서 음이항분포는 이항분포와 반대 개념이라는 것을 유추할 수 있을 것 같습니다! 전체 시행 횟수를 $n$, 성공횟수 $r$이라 하고, $\small X\sim NB(r,p),\space Y\sim B(n,p)$이라 할때, 실제로 확률변수 $X$와 $Y$는 다음의 관계를 가지고 있습니다.
\[P(X\le n) = P(Y\ge r)\]좌변은 $r$개의 성공을 거두는 데 $n$ 이하의 시행 횟수가 필요한 사건을 의미하고, 우변은 $n$개의 시행에서 $r$개 이상의 성공을 거두는 사건을 말합니다. 다시 말해서, $r$개의 성공을 거두는 데 $n$ 이하의 시행 횟수가 필요했다면, $n$개의 시행동안 $r$번 성공했거나, 아니면 그 이상 더 성공했을 수도 있을 것입니다. 즉, 음이항 분포에서는 시행 횟수 $n$이 확률변수이고 성공 횟수 $r$이 고정되어 있는 반면, 이항분포에서는 시행 횟수 $n$이 고정되어 있고 성공 횟수 $r$이 확률변수인 것입니다. 둘의 기준점이 다르다고 할 수 있겠네요!
실패 횟수로 표현한 음이항분포
그런데 음이항분포는 다음과 같이 $r$번째 성공을 얻기 위해 걸렸던 실패 횟수, $Y=X-r$의 함수로 나타내기도 합니다. 이렇게 하면, 가능한 y의 값은 0부터 시작할 것입니다!
\[\begin{gathered} f_Y(y)=\binom{y+r-1}{y}p^r(1-p)^y, \space y=0, 1, \cdots \cr (\because X=Y+r, \space \binom{y+r-1}{r-1} =\binom{y+r-1}{y} )\end{gathered}\]일단 $f_X(x)$에 변수변환을 통해 $f_Y(y)$을 구했는데요. 실제로 $f_Y(y)$가 $pmf$의 성질을 만족하는지 확인해보겠습니다. 즉, $\small \sum_{y=0}^\infty f_Y(y)=1$이 되는지 확인해보겠습니다.
\[\begin{aligned} \sum_{y=0}^\infty \binom{y+r-1}{y}p^r (1-p)^y &\overset{(1)}{=}p^r\sum_{y=0}^\infty \binom{-r}{y}(-(1-p))^y \cr &\overset{(2)}{=}p^r\cdot [1-(1-p)]^{-r} \cr &=1\end{aligned}\] \[\begin{aligned} (1)\space \binom{-r}{y} &= (-1)^y\cdot \binom{y+r-1}{y} \cr \because \binom{-r}{y} &= \frac{(-r)(-r-1)\cdots (-r-y+1)}{y!} \cr &= \frac{(-1)^y\cdot r(r+1)\cdots (r+y-1)}{y!} \cr &= (-1)^y\cdot \binom{y+r-1}{y} \cr (2)\space Binom&ial\space Theorem\cr (1-x)^{-s} &= \sum_{k=0}^\infty\binom{-s}{k} (-x)^k \space for \space s>0 \end{aligned}\]$Y$의 기대값과 분산 은 $Y=X-r$이라는 것을 이용하면 다음과 같이 될 것입니다.
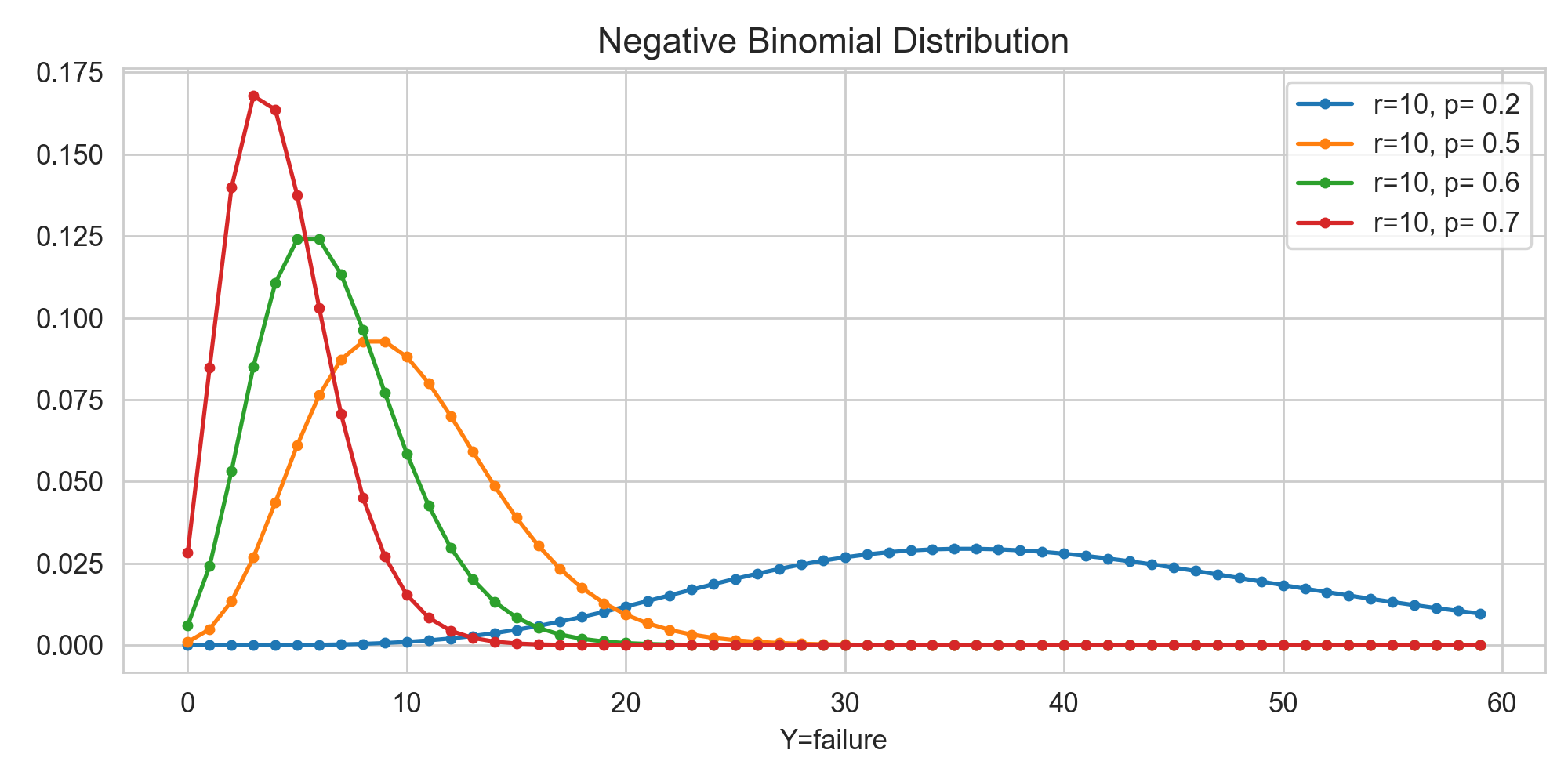
\[\begin{aligned} E(Y) &= E(X)-r = \frac{r}{p}-r = r\frac{1-p}{p} \cr Var(Y) &= Var(X) = r\frac{1-p}{p^2} \end{aligned}\]아래 그림은 성공 횟수$(r)$ 10번을 얻기 위해 걸리는 실패 횟수$(Y)$의 확률값에 대한 분포입니다. 성공확률이 클수록 실패 횟수가 적게 필요할 확률이 높은 것을 확인할 수 있고, 성공 확률이 낮을수록 실패 횟수가 대체로 많이 필요하며, 분산이 크고 넓게 퍼져있는 것을 확인할 수 있습니다.
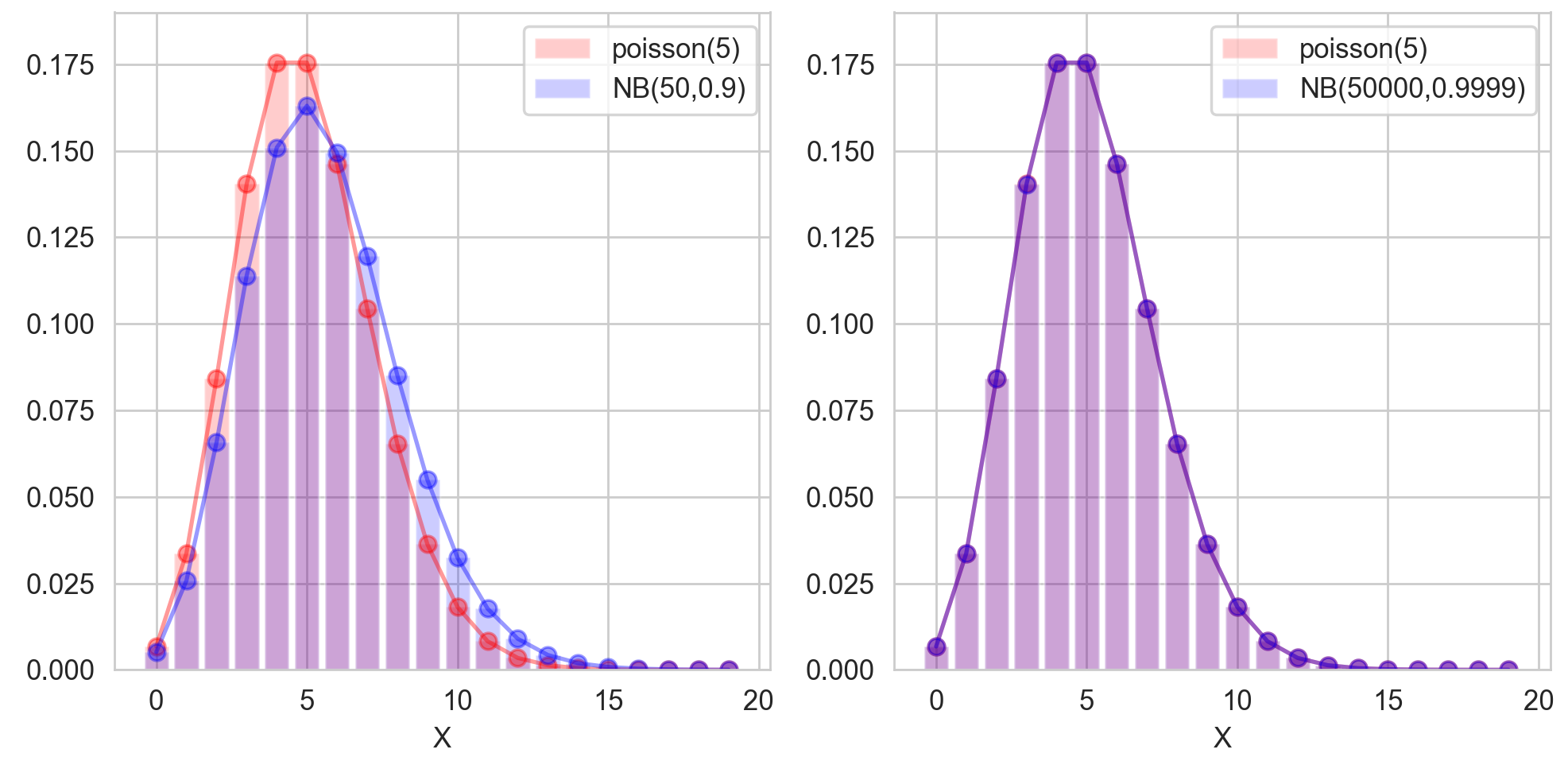
음이항분포의 포아송분포로의 근사
한편, 음이항분포는 포아송 분포로 수렴된다는 특징이 있습니다. 포아송 분포 포스트에서 이항 분포는 포아송 분포로 수렴된다는 것을 보였었는데요. 역시나 음이항 분포는 이항분포랑 짝꿍이라고 음이항 분포 역시 포아송 분포로 수렴합니다! 구체적으로 확률변수 $\small X\sim NB(r,p)$이고, $\small r\rightarrow \infty,\space p\rightarrow 1,\space r(1-p)\rightarrow \lambda$일 때, $\small Poisson(\lambda)$에 수렴하게 됩니다. 이걸 이제 증명해봅시다. 증명하는 방식은 음이항분포의 적률생성함수가 포아송 분포의 적률생성함수에 수렴하는 것을 보이는 것입니다. 따라서 먼저 음이항 분포의 적률생성함수를 구해봅시다.
원래 적률생성함수를 구하기 위해서는 $E(e^{tY})$를 구해야 하지만, $E(t^Y)$를 먼저 구하겠습니다. 계산이 훨씬 편리해집니다! 그 후에 $t$ 자리에 $e^t$를 넣어주면 됩니다.
\[\begin{gathered} G_Y(t) := E(t^Y)=E(e^{Y\cdot \log t})=M_Y(\log t) \cr \implies M_Y(t) = G_Y(e^t) \end{gathered}\]이제 위에서 정의한 $G_Y(t)$를 구하고, 그 뒤에 $M_Y(t)$를 구해보겠습니다.
\[\begin{aligned} G_Y(t) &= \sum_{y=0}^\infty t^y\cdot \binom{y+r-1}{y} p^r (1-p)^y\cr &=p^r \sum_{y=0}^\infty \binom{y+r-1}{y} [t(1-p)]^y \cr &= p^r \cdot [1-t(1-p)]^{-r}\cr &= \big\lbrack\frac{p}{1-t(1-p)} \big\rbrack ^{r},\space \vert t\vert < \frac{1}{1-p}\cr \therefore M_Y(t) &= G_Y(e^t)= \big\lbrack\frac{p}{1-e^t(1-p)} \big\rbrack ^{r}, \space e^t < \frac{1}{1-p}\end{aligned}\]이렇게 적률생성함수를 구했습니다. 이제 음이항분포의 적률생성함수가 포아송분포의 적률생성함수로 수렴하는 것을 증명해봅시다. $r(1-p)$이 $\lambda$에 수렴한다는 조건은 다음과 같이 정리될 수 있을 것입니다.
\[\begin{aligned} r(1-p) &\rightarrow \lambda \cr r(1-p) &= \lambda +o(1) \cr \implies p&=1-\frac{\lambda}{r} +o(\frac{1}{r}) \cr \frac{o(\frac{1}{r})}{\frac{1}{r} } \rightarrow & 0 \space as \space r\rightarrow \infty \end{aligned}\]위에서 정리한 내용을 잘 기억해서 이제 진짜로 증명해봅시다!
\[\begin{aligned} M_Y(t) &= \big\lbrack\frac{p}{1-e^t(1-p)} \big\rbrack ^{r}\cr &=\bigg\lbrack \frac{1-\frac{\lambda}{r}+o(\frac{1}{r})}{1-\frac{e^t\lambda}{r}+o(\frac{1}{r})} \bigg\rbrack ^r \cr &= \bigg\lbrack 1+ \frac{\frac{(e^t-1)\lambda}{r}+o(\frac{1}{r})}{1-\frac{e^t\lambda}{r}+o(\frac{1}{r})} \bigg\rbrack ^r \cr &= \bigg\lbrack 1+ \frac{1}{r}\bigg ( \frac{ (e^t-1)\lambda+o(1) }{ 1-\frac{e^t\lambda}{r}+o(\frac{1}{r})} \bigg ) \bigg\rbrack ^r \cr &\longrightarrow e^{\lambda(e^t-1)}\end{aligned}\]위와 같이 음이항 분포의 적률생성함수가 포아송 분포의 적률생성함수에 수렴하게 되는 것을 확인했습니다. 성공 횟수가 무한대로 커지고, 실패 확률은 매우 작아지며 이들의 곱은 람다에 수렴하게 될 경우, 음이항 분포는 포아송 분포에 수렴하게 됩니다. 이항분포의 포아송 분포로의 근사에서는, 이항분포는 전체 시행 횟수가 무한히 커지고 성공 확률이 매우 작아서 이들의 곱이 람다에 수렴할 경우에 포아송 분포에 근사했다는 점에서 음이항분포랑 반대라는 것을 알 수 있습니다. 음이항분포에서는 전체 성공 횟수가 무한히 커질수록 필요한 실패 횟수라는 확률변수의 확률값을 계산하는 과정이 복잡해질 것입니다. 이 때, 전체 성공 횟수가 무한히 커지고, 실패할 확률이 매우 작다면, 이들의 곱을 평균 실패 횟수로 하는 포아송 분포를 통해 확률값을 보다 쉽게 구할 수 있게 됩니다.
$Reference$
- 송성주, 전명식. (2015). 수리통계학
- 고려대학교 송성주 교수님의 수업