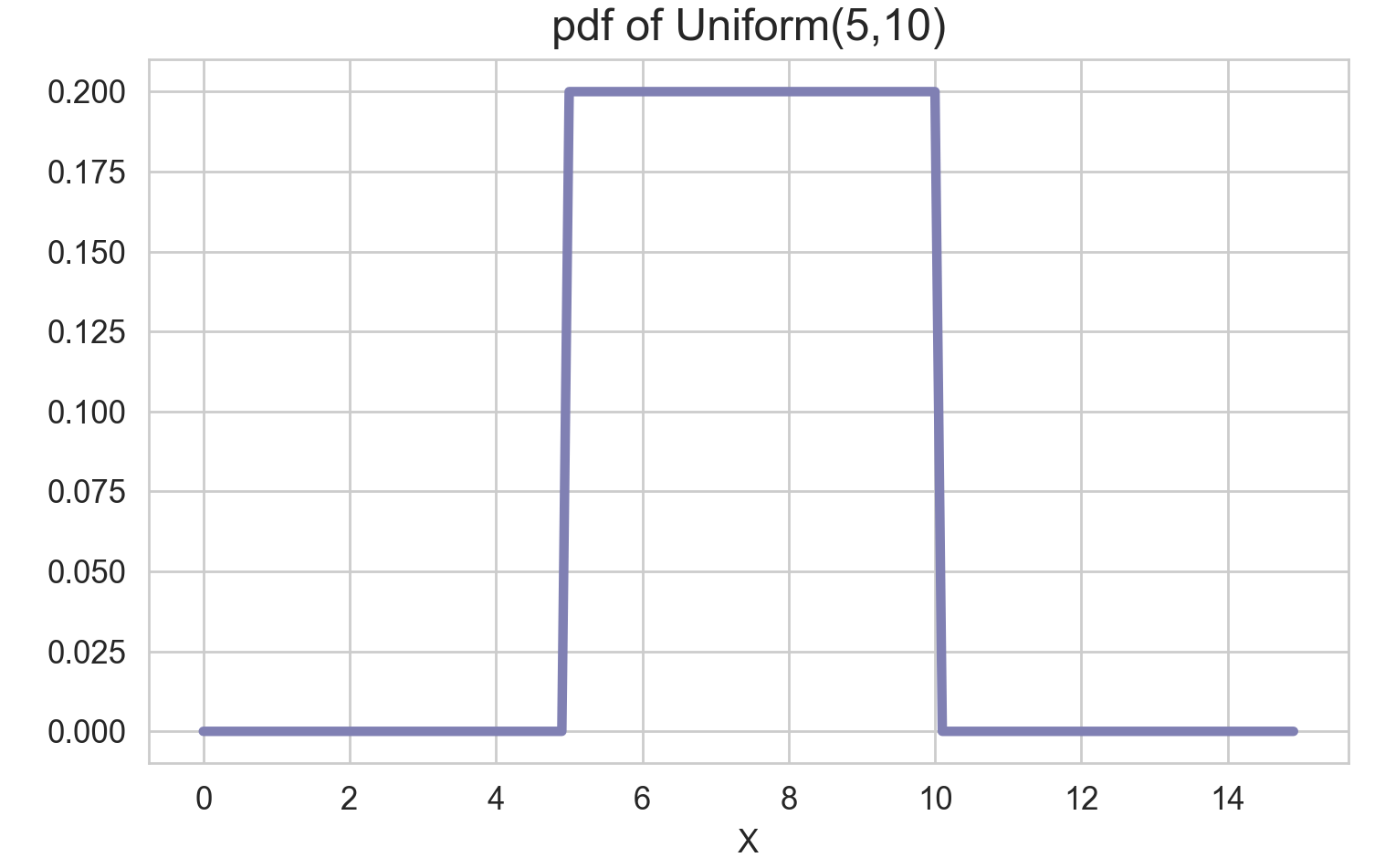
[연속형 분포] 균일 분포(Uniform distribution)
이번 포스트에서는 균일 분포(Uniform Distribution)에 대해 알아보고, 기대값과 분산, 적률생성함수를 구해보겠습니다.
균일 분포(Uniform Distribution)
균일 분포는 정해진 범위에서 모든 확률이 균일한 분포를 의미합니다. 가장 간단하면서도 응용도 많이 되는 분포입니다. 범위가 0에서 1사이일 때에는 하나의 지시 함수(Indicator function)로도 이용될 수 있습니다. 사실 균일 분포는 연속형 분포도 될 수 있지만 이산형 분포 버전도 있습니다! 이산형 균일 분포는 마찬가지로 가능한 $X$의 모든 값 $\lbrace x_1, x_2, \cdots, x_n \rbrace$에서 균일한 확률값을 가지는 분포일 것입니다. 이번 포스트에서는 연속형 균일 분포를 중점적으로 설명하려고 합니다. 연속형 균일 분포의 확률밀도함수는 다음과 같이 나타낼 수 있습니다.
이제 균일분포의 기대값과 분산을 구해보겠습니다. 다른 분포에 비해서 계산 과정이 매우 간단합니다.
\[\small\begin{aligned} E(X)&= \int_a^b \frac{1}{b-a}x \space dx \cr &= \frac{1}{b-a} \cdot \frac{1}{2} x^2 \bigg\vert^b_a =\frac{b+a}{2} \cr E(X^2) &= \int_a^b \frac{1}{b-a}x^2 \space dx \cr &= \frac{1}{b-a} \cdot \frac{1}{3}x^3 \bigg\vert^b_a =\frac{a^2+b^2+ab}{3} \cr Var(X)&= E(X^2)-E(X)^2 = \frac{(b-a)^2}{12}\end{aligned}\]이번엔 적률생성함수를 구해보겠습니다.
\[\begin{aligned} M_X(t) &= E(e^{tX}) = \int_a^b \frac{1}{b-a}e^{tx} \space dx \cr &= \frac{1}{b-a}\cdot \frac{1}{t}e^{tx} \bigg \vert^b_a = \frac{e^{tb}-e^{ta}}{t(b-a)}, \space (t\not =0 )\end{aligned}\]연속형 분포의 cdf는 Uniform(0,1)을 따른다.
이제 균일분포와 관련된 정리에 대해서 알아보고자 합니다.
Thm. $X$는 누적 확률밀도함수가 $F_X(x)$인 연속형 확률변수이다. 이 때, $Y=F_X(x)$라고 정의하자. $Y$는 $Uniform(0,1)$을 따른다. $(i.e. \space F_Y(y)=y, \space 0<y<1)$
누적 확률밀도함수는 무조건 증가함수일 것입니다. 이 때, 누적 확률밀도함수가 strictly increasing하다고 하면, 다시 말해서 중간에 평평한 구간 없이 계속 증가하는 형태라면 증명은 매우 간단합니다.
\[\begin{aligned} Let \space F_X(x) &\space be \space strictly \space increasing \space function. \cr F_Y(y)&= P(Y\le y) = P(F_X(x)\le y)\cr &=P(x\le F^{-1}_X(y)) \cr &= F_X(F^{-1}_X(y)) =y, \space (0<y<1)\end{aligned}\]하지만 평평한 구간이 있을 경우에는 $F_X(x)$가 역함수가 존재하지 않기 때문에 위와 같이 구할 수는 없습니다. 이 때에는 infimum을 이용해서 주로 풀이를 하는데 infimum과 관련된 내용은 이 포스트에서는 생략하겠습니다.
한편, 위 정리에 의하면 연속형 확률변수의 누적 확률밀도함수는 균일 분포를 따른다고 합니다. 예를 들어, 지수 분포로부터 랜덤으로 샘플들을 뽑고 그 값에 대한 누적 확률 밀도 함수가 0에서 1 사이의 균일 분포를 따른다는 것입니다.
$Reference$
- 송성주, 전명식. (2015). 수리통계학