[연속형 분포] 지수 분포(Exponential distribution)

About Mathematical Statistics

이번 포스트에서는 지수 분포(Exponential Distribution)에 대해서 정리하고자 합니다. 기대값, 분산을 구해보고 포아송 분포와의 관계, 그리고 무기억성 에 대해서 알아보겠습니다.

지수 분포(Exponential Distribution)

지수 분포는 특정한 사건이 일어나고, 그 다음에 같은 사건이 다시 일어날 때까지 걸리는 시간에 대한 분포입니다. 예를 들어 평균적으로 10분마다 도착하는 버스가 있을 때, 버스를 놓친 후 그 다음 버스가 올때까지 기다리는 시간은 지수 분포를 따른다고 할 수 있을 것입니다. 그런데, 이렇게 다음 사건이 발생할 때까지 기다리는 시간을 구하려면, 어떤 시간 단위에서 그 사건이 평균적으로 몇 번 발생하는지는 알아야 하지 않을까요? 다시 말해서, 특정 단위 구간에서 그 사건의 발생 횟수에 대한 분포를 알아야 할 것 같은데요. 그런데 이 분포 어디서 많이 보지 않았나요?! 바로 포아송 분포입니다! 어떤 사건의 발생 횟수가 포아송 분포를 따르면, 사건 사이의 대기 시간은 지수 분포를 따르게 됩니다.

어떤 사건 $A$의 발생 횟수가 발생률(rate, 평균 발생 건수)이 $\lambda$인 포아송 분포를 따를 때, $A$가 일어나고 그 다음에 또 일어날 때까지 걸리는 시간을 $W$라고 한다면, $W$는 음이 아닌 값을 가지는 연속형 확률변수가 될 것입니다. 이 때, $W$의 cdf는 다음과 같이 표현될 것입니다.

\[\begin{aligned} F_W(w) &= P(W\le w) , \quad (w\ge0)\cr &= 1-P(W>w)\cr &= 1-P[구간\space [0,w]에서\space A가\space 일어나지\space 않음 ] \cr &= 1-P[X=0 \space for \space time\space unit=1,2,\cdots , w] \cr &= 1-P[X=0 \space for\space time=1]\cdots P[X=0 \space for \space time=w] \cr &= 1-\bigg[ \frac{\lambda^0 e^{-\lambda}}{0!}\bigg]^w \cr &= 1-e^{-\lambda w},\quad (w\ge 0) \end{aligned}\]

이해되셨나요? 따라서 이를 미분하면 다음과 같이 대기 시간 $W$의 pdf를 구할 수 있습니다.

\[\begin{aligned} f_W(w) &=\frac{w}{dw} F_W(w)\cr &= \frac{w}{dw} [1-e^{- \lambda w}] \cr &= \lambda e^{-\lambda w}, \quad w\ge 0 \end{aligned}\]

위와 같은 pdf는 모수 $\lambda$를 포아송 분포의 모수와 같은 것으로 둬서 표현한 것입니다. 그런데 또 많은 경우에 지수 분포의 모수를 포아송 분포의 모수의 역수($\frac{1}{\lambda}$)로 두기도 합니다.

\[f_X(x) = \frac{1}{\lambda}e^{-\frac{1}{\lambda}x}, \space x\ge 0\]

왜 역수로 두는지는 아래 기대값과 분산을 구하면서 조금 더 자세히 설명하겠습니다. 일단 이번 포스트에서는 지수 분포의 모수를 포아송 분포의 모수와 같은 것으로 두겠습니다!

기대값과 분산

한편, 지수 분포는 감마 분포(Gamma Distribution)의 특수한 경우입니다. 감마 분포는 다음 포스트에서 다룰 예정이지만, 지수 분포는 $\alpha=1, \space \beta=\frac{1}{\lambda}$인 감마 분포라는 것을 이용하면 기대값 및 분산을 매우 쉽게 구할 수 있습니다.

\[EXP(\lambda) = Gamma(\alpha = 1, \beta = \frac{1}{\lambda})\] \[f_X(x) = \lambda e^{-\lambda x}, \space x\ge 0\]

따라서, $Gamma(\alpha, \beta)$의 기대값이 $\alpha \beta$이고, 분산이 $\alpha \beta^2$임을 고려할 때, 지수 분포의 기대값과 분산은 다음과 같이 됩니다.

\[\begin{aligned} E(X)&= \frac{1}{\lambda} \cr Var(X)&= \frac{1}{\lambda^2} \end{aligned}\]

하지만, 아무래도 포스트 순서 상 감마 분포를 먼저 안 다뤘으니 감마 분포를 이용하지 않고 기대값을 한번 구해보겠습니다! 계산은 부분 적분을 이용하면 됩니다. 분산을 구하는 과정은 기대값을 구하는 과정과 똑같으니 생략하겠습니다.

\[\begin{aligned} E(X) &= \int_0^\infty \lambda e^{-\lambda x} \cdot x \space dx \cr &= \big[ -e^{-\lambda x} x \big ]^\infty_0 - \int_0^\infty -e^{-\lambda x} \space dx \cr &= \big [- \frac{1}{\lambda}e^{-\lambda x} \big]^\infty_0 = \frac{1}{\lambda} \end{aligned}\]

어떤 사건이 평균 발생 수가 $\lambda$인 포아송 분포를 따를 때, 사건 사이의 평균 소요 시간은 그것의 역수 $\frac{1}{\lambda}$가 되는 것입니다! 왜일까요? 어떤 사건의 평균 발생 건수가 4라고 합시다. 즉, 특정 단위 시간에서 사건이 4번 일어나는 거니까, 평균적으로 한 사건이 일어나고 그 다음 사건이 일어나기까지 그 시간 단위의 $\frac{1}{4}$배 만큼의 시간이 소요된다는 것을 의미합니다. 따라서, 단위 구간에서 평균 사건 발생 수$(\lambda)$가 많아질 수록, 사건 사이 평균 소요 시간$(\frac{1}{\lambda})$은 짧아질 것이고, 이 소요 시간들의 차이는 크게 나지 않을 것입니다.

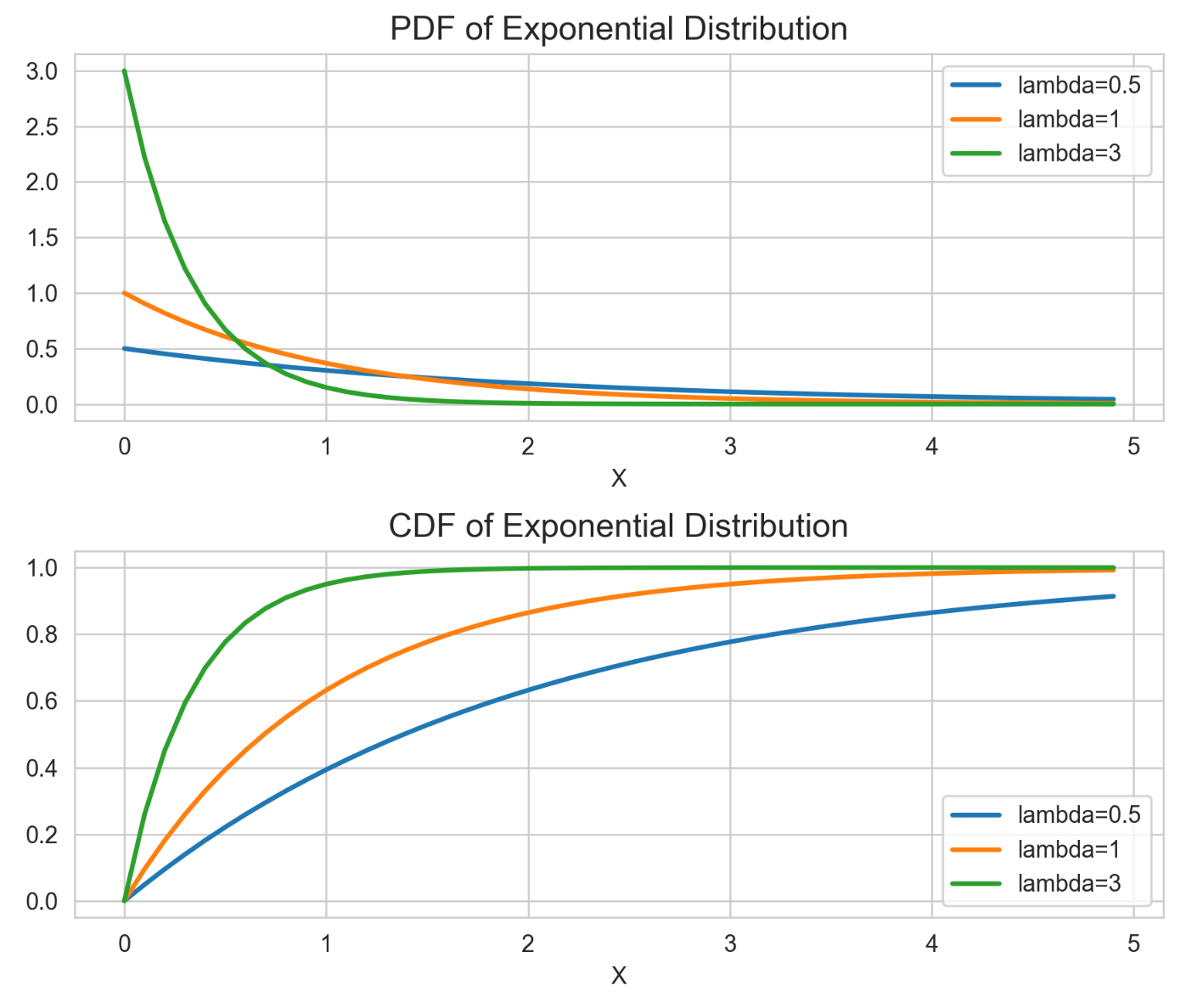
아래 그림에서 $\lambda$는 포아송 분포의 $\lambda$, 즉 사건의 평균 발생 빈도입니다. 사건의 평균 발생 빈도가 커질수록 사건 사이 평균 소요 시간은 짧아진다고 했습니다. 아래 누적 분포(cdf)를 보면, $\lambda=3$일 때, 즉 평균 발생 사건 수가 높을 수록 더욱 빨리 1에 가까워지는 것을 볼 수 있습니다. 즉, 더 낮은 소요 시간(X)에 대해 확률값들이 더욱 높았다는 것을 의미합니다.

무기억성 (Memoryless Property)

지수 분포 하면 빼 놓을 수 없는 성질이 바로 무기억성입니다. 다음의 식을 만족하면 무기억성 성질을 갖는다고 말합니다. 일단 식을 만족하는 것부터 확인해봅시다. 식의 증명은 정말 간단합니다!

\[P(X>a+t \vert X>a) = P(X>t), \space (a,t\ge 0)\] \[\begin{aligned} \therefore P(X> a+t \vert X >a ) &= \frac{P(X>a+t)}{P(X>a)} \cr &= \frac{e^{-\lambda (a+t)}}{e^{-\lambda a}} = e^{-\lambda t} \cr &=P(X>t) \end{aligned}\]

그러면 이제 ‘무기억성을 갖는다’는 것의 의미를 알아봅시다. 어떤 시점 부터 소요되는 시간은 과거 시간에 영향을 받지 않는다는 것입니다. 예를 들어, 지수 분포는 전구 수명과 관련하여 자주 언급되는데요. 어떤 전구를 한 달간 사용했을 때, 남은 전구 수명은 한 달 간 사용했던 것에 영향을 받지 않고, 그냥 새 전구의 남은 수명과 같다는 것입니다. 또 다른 예로 핸드폰을 5년 썼는데 고장나기 까지 걸리는 시간은, 처음 산 뒤 고장나기까지 걸리는 시간과 같다는 것입니다. 우리의 생활 상식으로 상당히 비합리적으로 보입니다. 실제로 지수 분포는 우리 실생활에서 인간 또는 제품의 수명을 모델링하기에는 너무 단순화된 분포입니다. 그래서 이렇게 위험률(hazard rate)이 일정한 지수 분포보다는 와이블 분포(Weibull Distribution)가 생존 분석 및 수명 모델링에 훨씬 유연하게 사용된다고 합니다.

한편, 지수 분포와 기하 분포가 상당히 닮지 않았나요? 물론 지수 분포는 연속형 분포이고, 기하 분포는 이산형 분포입니다. 그런데 지수 분포는 ‘어떤 사건이 일어나기까지 걸리는 시간’이고, 기하 분포는 ‘어떤 사건이 발생할 때까지 걸리는 시행 횟수’입니다. 또 한, 두 분포 공통적으로 무기억성을 갖고 있습니다. 즉, 지수 분포는 기하 분포의 연속형 버전이라고 할 수 있습니다!


$Reference$