[연속형 분포] 감마 분포(Gamma distribution)
이번 포스트에서는 연속형 분포의 일종인 감마 분포(Gamma Distribution) 에 대해 알아보겠습니다. 감마 분포의 기대값, 분산 및 적률생성함수를 구하고, 감마 분포와 포아송 분포와의 관계에 대해 정리하고자 합니다.
감마 함수(Gamma function)
감마 분포에 대해 알아보기 전에 먼저 감마 함수를 알아야 합니다! 감마 함수는 아래 공식과 같이 정의되는 함수인데요. 이 감마 함수는 수학자들이 팩토리얼 $\small n!=n(n-1)(n-2)\cdots$을 자연수에만 한정해서 적용하지 않고, 더 큰 수 체계에도 적용할 수 있는 방법을 고민하다가 나온 함수라고 합니다. 즉, 복소수 범위까지 일반화 된 팩토리얼인 것이죠! 저는 개인적으로 수학 문제 풀 때 감마함수를 자주 쓰는데요. 저렇게 생긴 적분이 나오면, 일일히 부분적분 이용해서 구할 필요 없이 감마함수 쓰면 계산이 후딱 끝나서 좋습니다ㅎㅎ
이 감마함수는 아래 세가지 식과 같이 계산됩니다. 이걸 증명하는 과정은 부분적분 이용해서 계산 노동 하다보면 쉽게 해결됩니다! 일단 감마함수에 대해서는 이 정도만 알고 넘어가겠습니다.
- $\Gamma(\alpha) = (\alpha-1)\Gamma(\alpha-1), \space (\alpha>1)$
- $ \Gamma(\alpha) = (\alpha-1)!$
- $\Gamma(\frac{1}{2}) = \sqrt\pi$
감마 분포(Gamma Distribution)
본격적으로 감마 분포에 대해서 알아보겠습니다. 감마 분포의 확률밀도함수는 다음과 같습니다.
\[\begin{gathered} X\sim Gamma(\alpha, \beta) \cr f_X(x) = \frac{1}{\beta^{\alpha} \Gamma(\alpha)}x^{\alpha-1}e^{-\frac{x}{\beta}}, \quad (x,\alpha ,\beta >0) \cr (\alpha: shape\space parameter, \beta: scale\space parameter) \end{gathered}\]감마 분포는 $\alpha$개의 사건이 일어날 때까지 걸리는 대기 시간에 대한 분포라고 합니다. 그런데 이거 어디서 많이 보지 않았나요? 저번 포스트에서 했던 지수 분포는 사건이 1번 일어날 때까지 걸리는 시간에 대한 것이었습니다. 바로 감마 분포는 지수 분포를 한 번의 사건이 아닌 여러 개의 사건으로 확장한 것이라고 할 수 있습니다. 저번 포스트에서도 언급했듯이, 지수 분포는 $\alpha =1$인 감마 분포인 것입니다. 그런데 그 전에!!! 저번 포스트에서는 지수 분포의 모수를 포아송 분포의 모수(평균 발생 건수)와 같은 것으로 뒀었는데요. 사실 많은 경우에 포아송 분포의 모수의 역수(사건 사이 평균 소요 시간)를 지수 분포의 모수로 표현하기도 합니다. 감마 분포에서는 통상적으로 위의 공식과 같이 쓰기 때문에, 후자의 경우가 더 일반적입니다. 그래서 다소 헷갈리지만, 이번 포스트에서는 지수 분포의 모수를 포아송 분포의 모수의 역수로 두겠습니다..! 즉, 모수가 $\beta$인 지수분포에서 $\beta$는 사건 사이 평균 소요시간을 의미합니다.
이 때, 모수가 $\beta$인 지수 분포를 따르는 서로 독립이고 동일한(iid) 확률 변수 $\alpha$개를 합한 확률변수는, 모수가 $\alpha$와 $\beta$인 감마 분포 를 따릅니다!
그럼 이제 감마 분포의 기대값과 분산 을 구해보겠습니다.
\[\begin{aligned} E(X) &= \int_0^\infty \frac{1}{\beta^{\alpha} \Gamma(\alpha)}x^{\alpha-1}e^{-\frac{x}{\beta}} \cdot x\space dx \cr &=\frac{1}{\beta^{\alpha} \Gamma(\alpha)} \int_0^\infty x^{\alpha}e^{-\frac{x}{\beta}} dx, \space (t:=\frac{x}{\beta}\rightarrow dx=\beta dt) \cr &= \frac{1}{\beta^{\alpha} \Gamma(\alpha)} \int_0^\infty (\beta t)^{\alpha}e^{-t} \beta\space dt \cr &=\frac{\beta}{\Gamma(\alpha)} \int_0^\infty t^{\alpha}e^{-t} \space dt \cr &= \beta \frac{\Gamma(\alpha +1)}{\Gamma(\alpha)}= \alpha \beta \cr E(X^2) &=\int_0^\infty \frac{1}{\beta^{\alpha} \Gamma(\alpha)}x^{\alpha-1}e^{-\frac{x}{\beta}} \cdot x^2\space dx \cr &= \frac{1}{\beta^{\alpha} \Gamma(\alpha)} \int_0^\infty x^{\alpha +1}e^{-\frac{x}{\beta}} dx, \space (t:=\frac{x}{\beta}\rightarrow dx=\beta dt) \cr &= \frac{1}{\beta^{\alpha} \Gamma(\alpha)} \int_0^\infty (\beta t)^{\alpha +1}e^{-t} \beta\space dt \cr &= \beta^2 \frac{\Gamma(\alpha +2)}{\Gamma(\alpha)} = \alpha (\alpha +1)\beta^2 \cr Var(X) &= E(X^2) - E(X)^2 \cr &= \alpha(\alpha+1)\beta^2 -\alpha^2\beta^2 =\alpha\beta^2\end{aligned}\]감마 분포의 적률생성함수 도 구해보겠습니다!
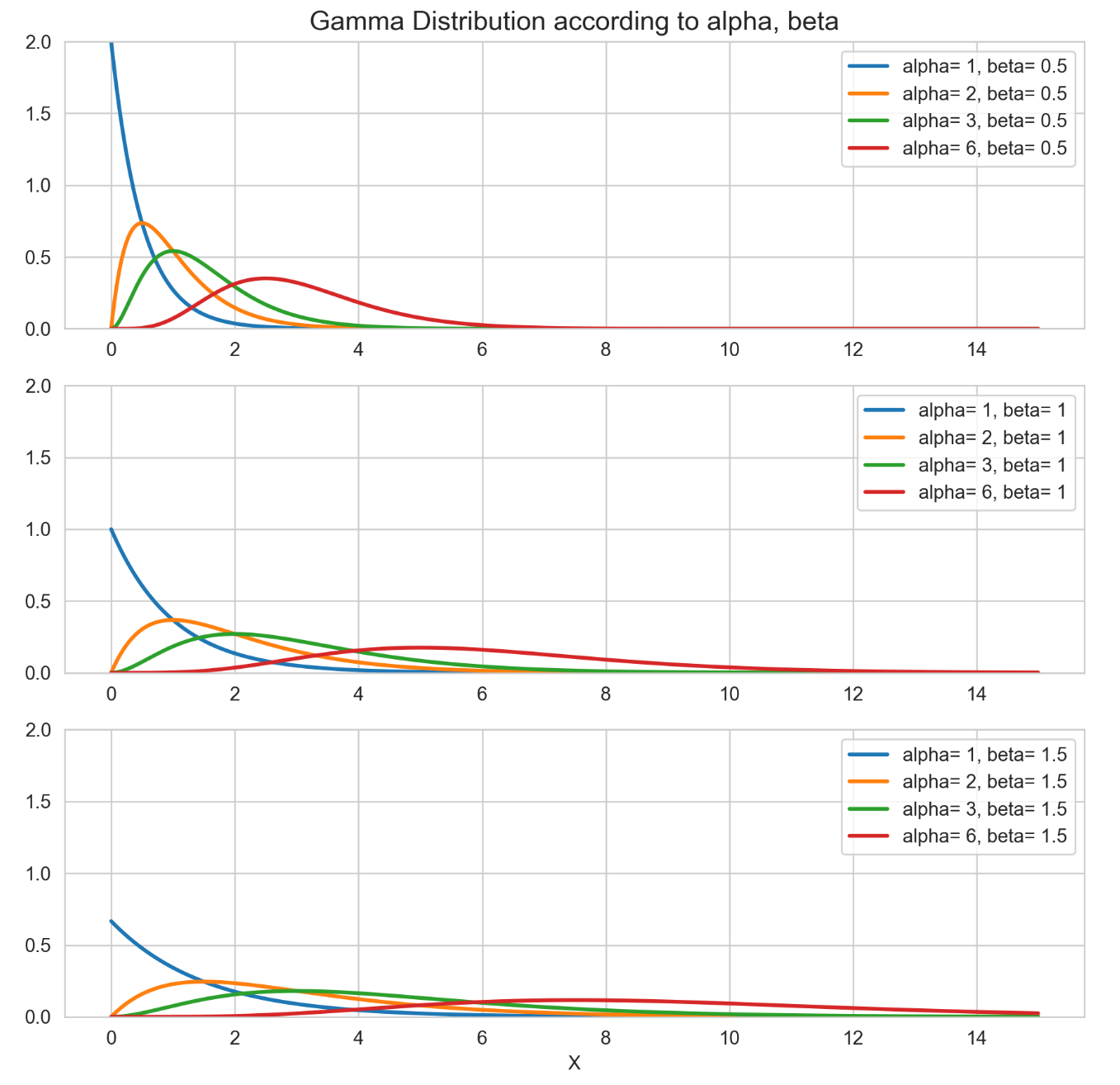
\[\begin{aligned} M_X(t) &= \int_0^\infty \frac{1}{\beta^{\alpha} \Gamma(\alpha)}x^{\alpha-1}e^{-\frac{x}{\beta}} \cdot e^{tx}\space dx \cr &= \int_0^\infty \frac{1}{\beta^{\alpha} \Gamma(\alpha)}x^{\alpha-1}e^{-\frac{1-\beta t}{\beta}x} \space dx, \space (t<\frac{1}{\beta}) \cr (z:=&\frac{1-\beta t}{\beta}x\rightarrow x=\frac{\beta}{1-\beta t}z, \space dx=\frac{\beta}{1-\beta t} dz) \cr &= \frac{1}{\beta^\alpha \Gamma(\alpha)} \int_0^\infty (\frac{\beta}{1-\beta t}z)^{\alpha -1} e^{-z} \frac{\beta}{1-\beta t} \space dz \cr &= \frac{1}{(1-\beta t)^\alpha} \frac{1}{\Gamma(\alpha)} \int_0^\infty z^{\alpha -1} e^{-z} \space dz \cr &= (1-\beta t)^{-\alpha} , \space t<\frac{1}{\beta} \end{aligned}\]아래는 각 모수 $\alpha, \beta$에 따른 감마 분포입니다. $\beta$가 고정되어 있는 상태에서 $\alpha$가 증가할수록 평균과 분산이 커지면서 점점 오른쪽으로 퍼지는 형태라는 것을 알 수 있습니다. 이 때, $\beta$를 증가하면 증가할수록 이 경향은 심해집니다. $\beta$가 증가할수록 분산이 훨씬 커지게 되어 더욱 퍼지는 형태가 된다는 것을 확인할 수 있습니다. 직관적으로도 기다릴 사건 개수($\alpha$)가 많아질수록, 사건 사이 평균 소요시간($\beta$)이 커질수록 전체 대기 시간이 길어질 것입니다.
감마 분포와 포아송 분포의 관계
저번 포스트에서 지수 분포와 포아송 분포가 밀접한 관련이 있다는 것을 알게 되었는데요. 감마 분포는 지수 분포를 확장한 것이므로, 감마 분포 역시 포아송 분포와 밀접한 관련이 있습니다. 실제로 감마 분포와 포아송 분포는 다음의 관계를 가지고 있습니다.
$X\sim Gamma(\alpha, \beta)$라고 하자. 이 때, 어떠한 $x$에 대해 $Y\sim Possion(\frac{x}{\beta})$라면, 다음의 관계가 만족된다. \(P(X\le x) = P(Y\ge \alpha)\)
먼저 직관적인 의미부터 이해해봅시다. 좌변은 사건 사이 평균 소요 시간이 $\beta$인 사건이 $\alpha$개 일어날 때까지의 소요 시간이 $x$보다 작거나 같을 확률입니다. 한편, 전체 소요 시간을 사건 사이 평균 소요 시간으로 나눈 것, 즉 $x/\beta$는 사건의 개수가 될 것입니다. 따라서 우변은 평균 발생 건수를 $x/\beta$로 하는 포아송 분포에서 사건이 $\alpha$개 이상 일어날 확률을 의미합니다. 즉, 사건이 $\alpha$개 일어나는데 걸렸던 시간이 $x$ 이하라는 것은, $x$ 시간 동안 사건이 $\alpha$개 일어나거나 또는 그 이상 일어났다는 것과 같을 것입니다. 다시 말해서, 좌변은 소요 시간 $x$가 확률변수이지만, 우변에서는 고정된 것입니다. 이제 이 관계를 수리적으로 증명하고 감마 분포 포스트를 마치겠습니다!
\[\begin{aligned} P(X\le x) &= \int_0^x \frac{1}{\Gamma(\alpha)\beta^\alpha} t^{\alpha -1} e^{-\frac{t}{\beta}} \space dt \cr &= \frac{1}{\Gamma(\alpha)\beta^\alpha} \big [ -\beta e^{-\frac{t}{\beta}}t^{\alpha -1} \big]^x_0 +\int_0^x\beta e^{-\frac{t}{\beta}} (\alpha-1)t^{\alpha -2} \space dt \cr &= \frac{1}{\Gamma(\alpha)\beta^\alpha}(-\beta e^{-\frac{x}{\beta}}x^{\alpha -1 }) + \frac{1}{\Gamma(\alpha -1)\beta^{\alpha-1}}\int_0^x t^{\alpha -2}e^{-\frac{t}{\beta}} \space dt \cr &= \cdots \cr &= - \frac{e^{-\frac{x}{\beta}}x^{\alpha -1}}{\Gamma(\alpha)\beta^{\alpha -1}} - \frac{e^{-\frac{x}{\beta}}x^{\alpha -2}}{\Gamma(\alpha -1)\beta^{\alpha -2}} - \cdots -\frac{e^{-\frac{x}{\beta}}x}{\beta} + \int_0^x \frac{e^{-\frac{t}{\beta}}}{\beta} \space dt \cr &= 1- \frac{e^{-\frac{x}{\beta}}(x/\beta)^{\alpha -1}}{(\alpha -1)!} - \frac{e^{-\frac{x}{\beta}}(x/\beta)^{\alpha -2}}{(\alpha -2)!} - \cdots -e^{-x/\beta} \cr &= 1 - P(Y=\alpha-1) -\cdots -P(Y=0) \cr &=1-P(Y\le \alpha -1) \cr &= P(Y\ge \alpha) \end{aligned}\]$Reference$
- 송성주, 전명식. (2015). 수리통계학
- 고려대학교 송성주 교수님의 수업