[연속형 분포] 베타 분포(Beta distribution)

About Mathematical Statistics

이번 포스트의 주제는 베타 분포(Beta Distribution)입니다. 베타 분포의 의미를 이해하고, 기대값, 분산, 적률생성함수를 구해 보고자 합니다.

베타 분포(Beta Distribution)의 PDF

베타 분포는 확률에 대한 확률 분포입니다. 베타 분포의 의미를 이해해보기 전에 먼저 베타 분포의 확률밀도함수를 한번 뜯어(?)보겠습니다! 베타 분포의 확률밀도함수는 다음과 같습니다.

\[\begin{gathered} X\sim Beta(\alpha, \beta)\cr f_X(x)=\frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta -1}\cr (0<x<1,\space \alpha,\beta >0) \end{gathered}\]

이전에 했던 연속형 분포 지수 분포와 감마 분포는 대기 시간에 대한 분포였습니다. 그래서 도메인 즉, x의 범위가 ‘0 보다 큰 것’이었는데요. 베타 분포는 확률에 대한 분포이기 때문에, x의 도메인이 ‘0에서 1 사이’ 입니다! 한편, 거듭제곱 $\alpha-1, \beta-1$는 각각 어떤 사건의 ‘성공 횟수’, ‘실패 횟수’로 여길 수 있습니다. 그런데 $x$ 앞에 있는 $B(\alpha, \beta)$는 무엇일까요? 확률밀도함수의 0부터 1사이 integral sum이 1이 되도록 하는 상수입니다.

\[\begin{aligned}1 &= \int_0^1 \frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta -1}\space dx\cr B(\alpha, \beta) &=\int_0^1 x^{\alpha -1}(1-x)^{\beta -1}\space dx \end{aligned}\]

그런데 이 상수는 저번 포스트에서 했던 감마함수로 표현됩니다!

\[B(\alpha, \beta)= \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha + \beta)}\]

어떻게 감마함수의 분수로 계산되는지 증명해보겠습니다!

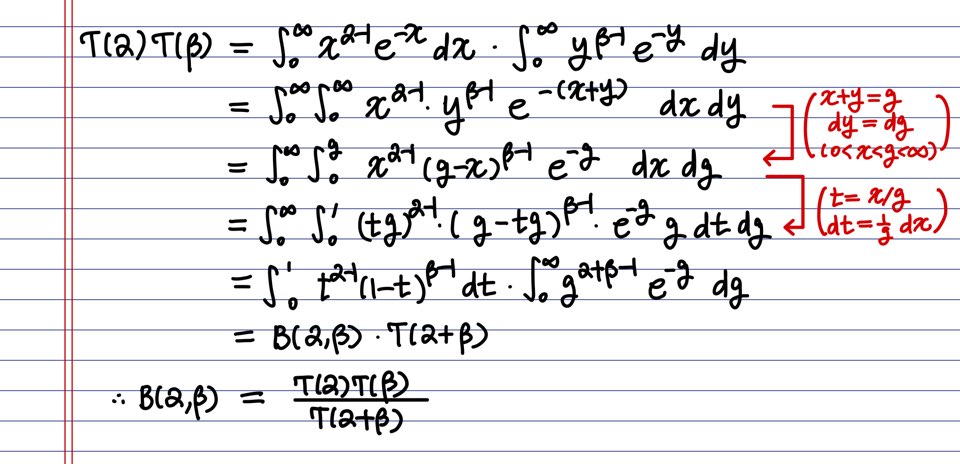
베타 분포의 이해

베타 분포의 확률밀도함수가 어떻게 생겼는지 먼저 확인해보았는데요. 이제 베타 분포를 조금 더 이해해보고자 합니다. 베타 분포는 확률에 대한 확률 분포라고 했습니다. 그렇다면 베타 분포를 적용할 수 있는 예가 뭐가 있을까요? 이 포스트를 읽은 방문자 중 이 포스트의 공감 버튼을 누를 확률이 0.5보다 클 확률을 구하고 싶을 때 베타 분포를 이용할 수 있을 것입니다. 예를 들어, 지금까지 포스트를 읽은 사람 3명은 공감 버튼을 누르고, 10명은 공감 버튼을 누르지 않았다면, 이 포스트를 읽게 될 사람이 공감 버튼을 누를 확률이 0.5보다 클 확률은 다음과 같이 계산될 것입니다. 확률이 약 0.02밖에 안되네요..!

\[\begin{aligned} P(X>0.5)&=1-P(X<0.5)\cr &= 1-\int_{0}^{0.5} \frac{\Gamma(13)}{\Gamma(3)\Gamma(10)} x^{3-1}(1-x)^{10-1}\space dx \cr &= 0.01929 \end{aligned}\]

그런데 베타 분포의 확률밀도함수에서 앞의 상수항만 떼고 보면 어디서 본 것 같은 식이지 않나요? 성공 확률의 거듭 제곱과 실패 확률의 거듭 제곱의 곱은 이항 분포(Binomial Distribution)의 확률질량함수에서도 볼 수 있었습니다! 그런데, 이항 분포에서는 확률 $p$가 고정된 것이고, 성공 횟수 및 실패 횟수가 확률변수였던 반면, 베타 분포에서는 성공 횟수$\small (\alpha-1)$와 실패 횟수$\small (\beta -1)$가 고정된 것이고, 확률이 확률변수입니다!

\[\begin{aligned} beta &: x^{\alpha -1}(1-x)^{\beta -1} \cr binomial &: p^{x}(1-p)^{n-x} \end{aligned}\]

실제로 베타 분포는 베이지안 방법에서 이항 분포의 켤레 사전 분포(Conjugate Prior Distribution)로 활용됩니다. 베이지안 방법이라는 것은 모수를 확률변수로 생각하여, 그에 대한 사전 정보를 활용하여 모수를 추정하는 방법입니다. 이 때, 이항 분포의 모수를 추정하는 데 있어 베타 분포가 사전 분포로써 이용됩니다.


기대값, 분산, 적률생성함수

이제 베타 분포의 기대값, 분산, 적률생성함수를 모두 구해보겠습니다.


한편, 베타 분포는 $\alpha, \beta$의 값에 따라 정규분포와 비슷한 형태, 직선, U자 모양 등 매우 다양한 형태를 띄고 있습니다. 각 $\alpha , \beta$에 따른 플랏을 아래 그려보았습니다.

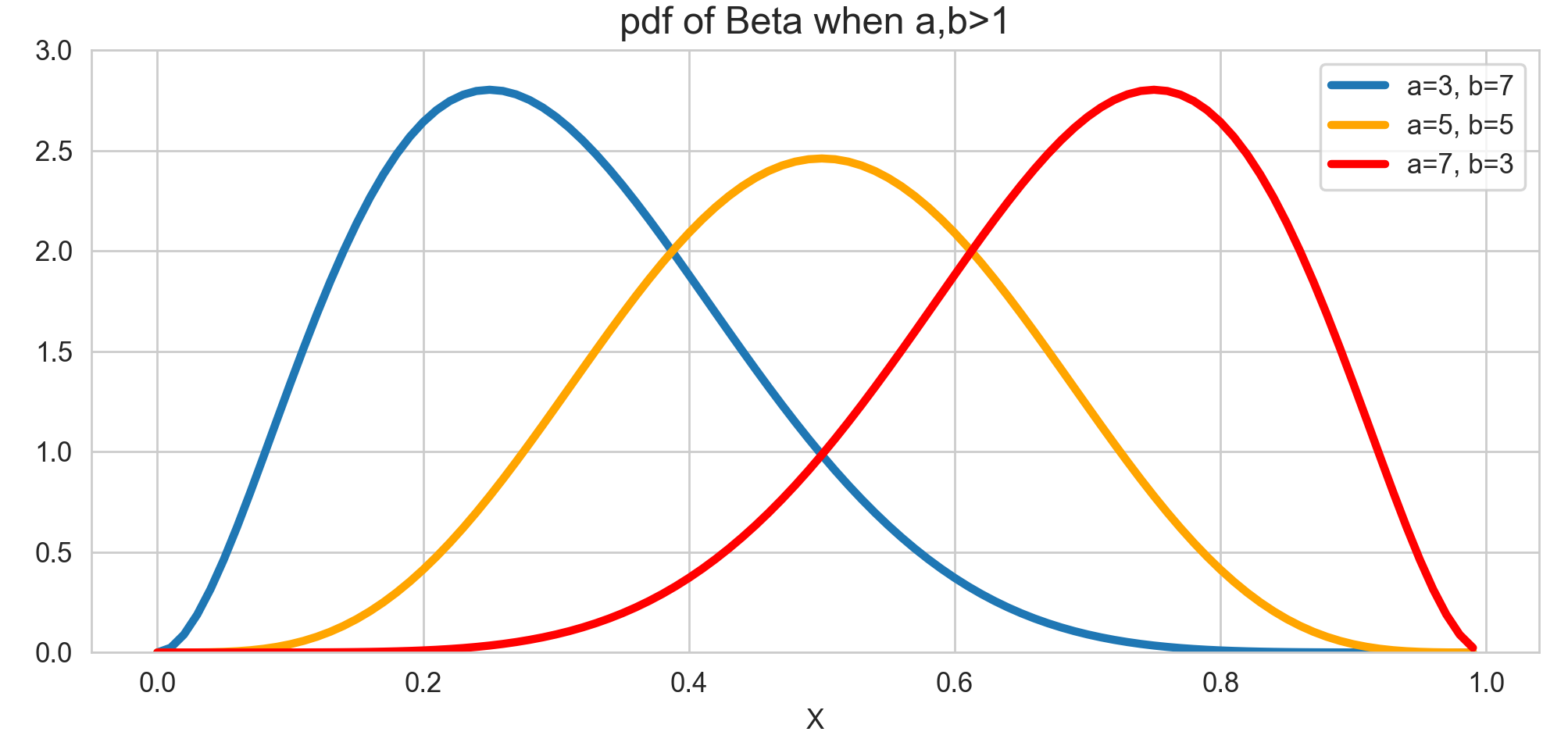
  • $\alpha, \beta$가 모두 1보다 클 때

    세 경우 모두 기대값에서 가장 높은 봉우리를 가지는 것을 확인할 수 있습니다. 또 한, $\alpha, \beta$가 같을수록 분산의 분자가 커져서 분산이 커지는 것을 확인할 수 있습니다. 실제로 $\alpha +\beta$가 커지고, $\alpha, \beta$의 값이 서로 비슷할수록 정규분포에 점근적으로 근사한다고 합니다. 이는 나중에 정규분포 포스팅에서 확인해보겠습니다.

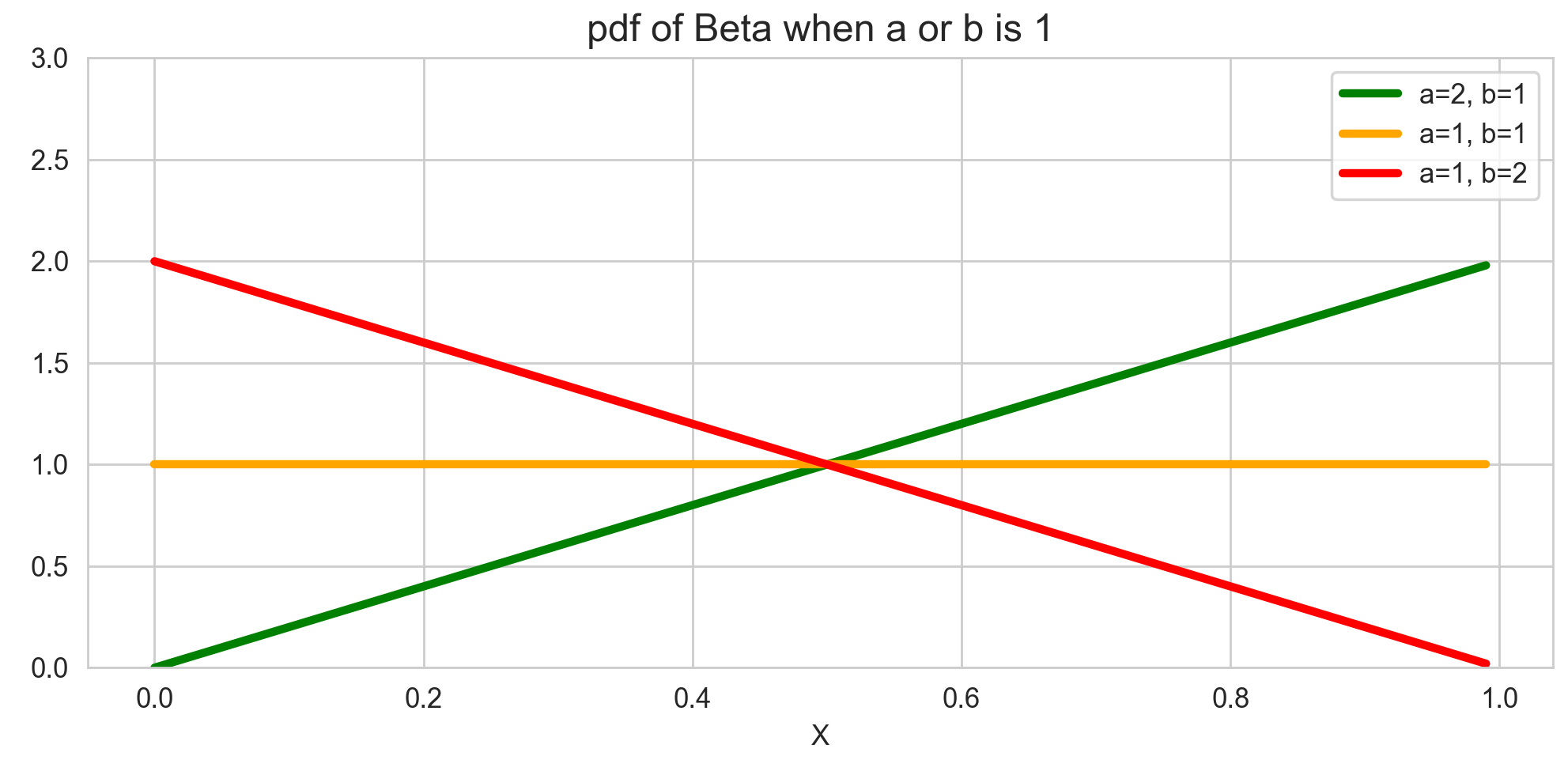
  • $\alpha, \beta$ 중 하나 이상이 1일 때

    위 플랏을 보면, $\alpha = \beta =1$일 때 베타 분포는 균일분포, 즉 Uniform(0,1)을 따르는 것을 확인할 수 있습니다. 왜 그럴까요? 이 경우 성공횟수, 실패 횟수가 모두 0이라는 것이고, 성공 확률($x$) 값은 그에 따라 0부터 1까지 아무 숫자나 될 수 있을 것입니다. 따라서 0부터 1까지 모든 확률이 균일한 균일분포가 될 것입니다. 반면, $\alpha=2, \beta=1$인 경우에는, 성공횟수가 1이고 실패 횟수가 0이기 때문에, 성공 확률이 높을 가능성이 높을 것입니다.

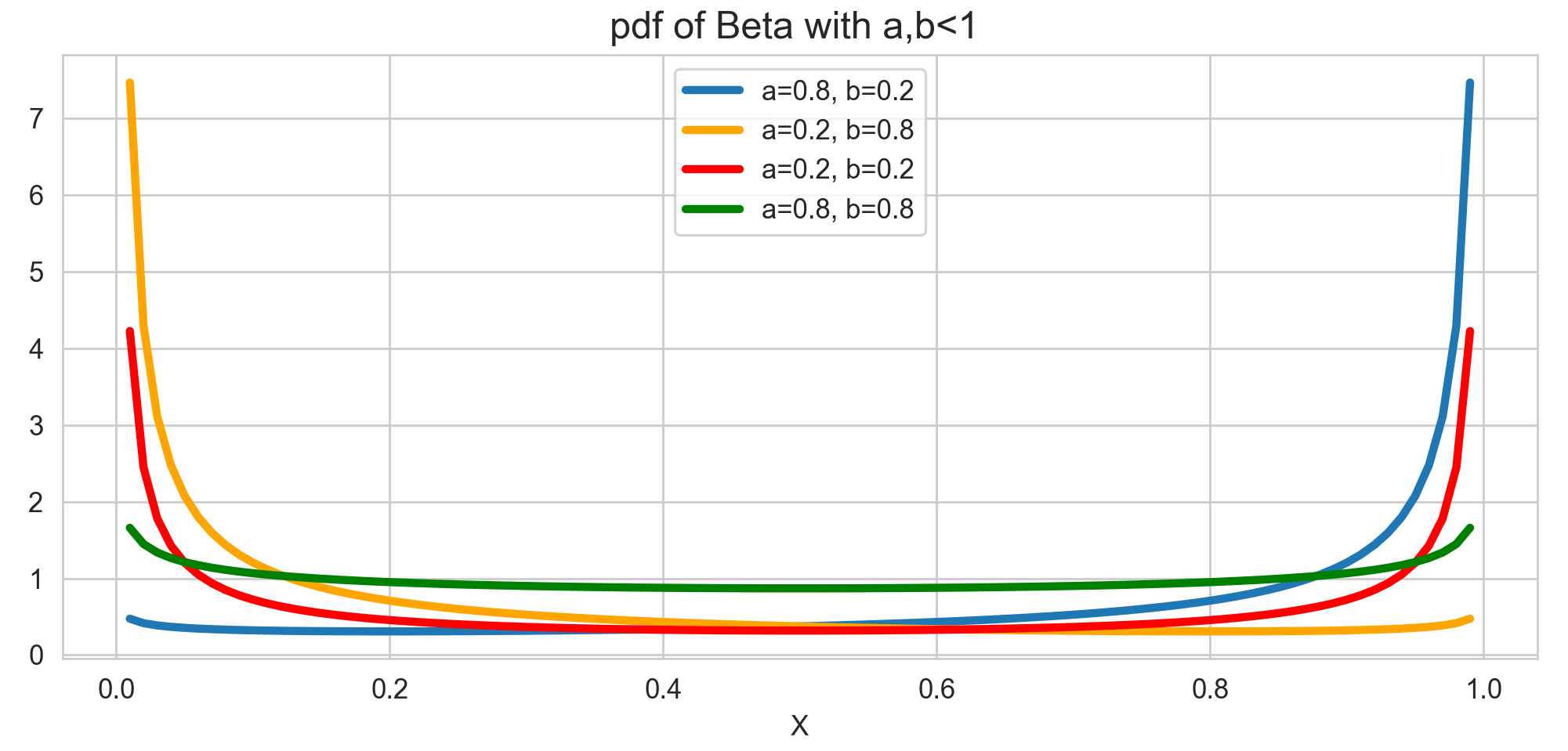
  • $\alpha, \beta$가 모두 1보다 작을 때

    $\alpha, \beta$가 모두 1보다 작을 때에는 U자 모양을 띄고 있는 것을 확인할 수 있습니다. 이 경우는 성공 횟수와 실패 횟수로 어떻게 해석해야 할지는 모르겠습니다. 다만, $\alpha, \beta$가 1에 가까워질수록 균일 분포에 가까워지는 반면, 0에 가까워질수록 성공 확률이 0 또는 1, 극으로 치우칠 가능성이 높아지는 것 같습니다.

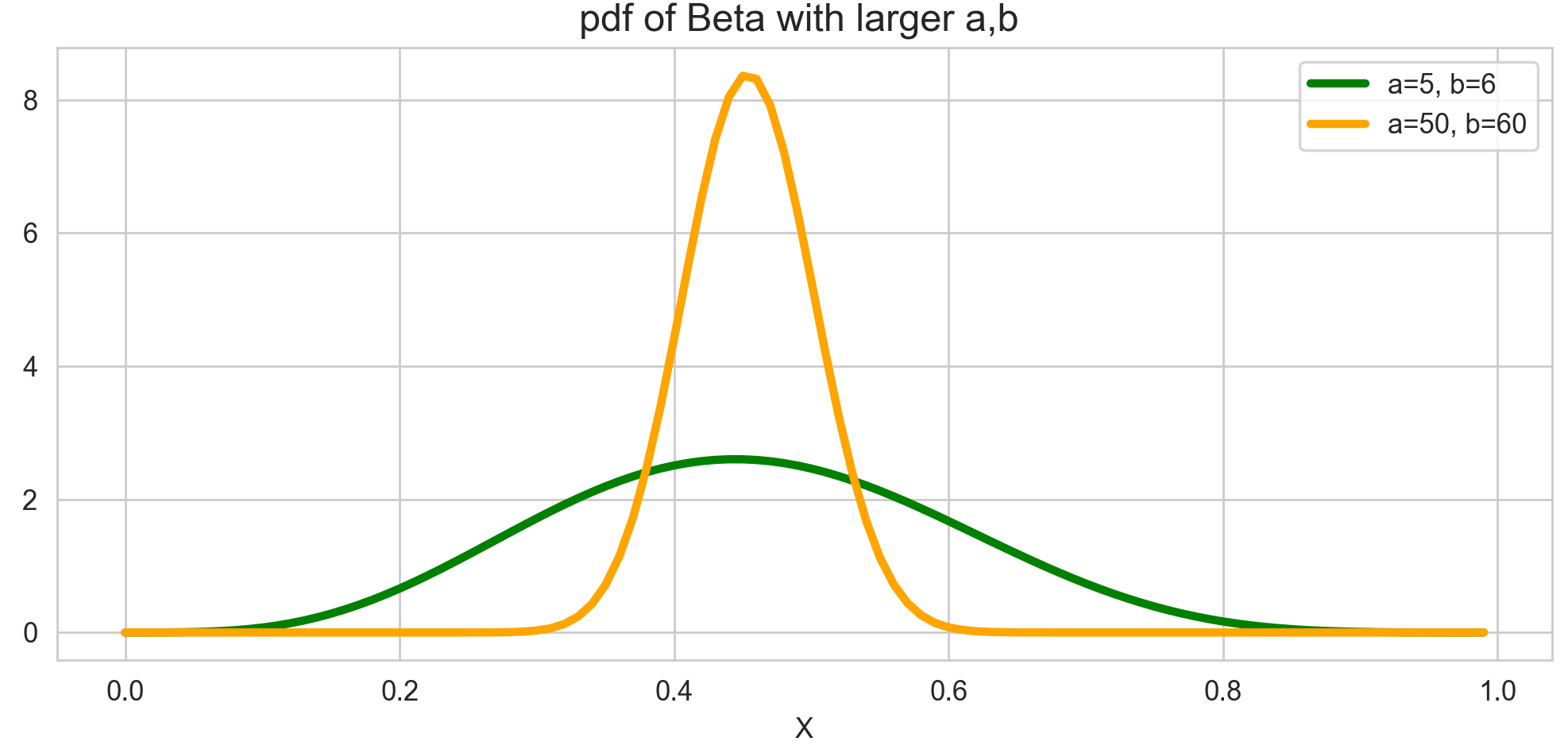
  • $\alpha, \beta$가 커지면?

    이 경우 기대값은 서로 같지만 분산의 차이가 있는 것을 확인할 수 있습니다. 이는 위에서 구한 기대값과 분산 공식을 생각하면 이해가 됩니다. 기대값은 $\alpha$와 $\beta$의 비율이기 때문에 위의 두 경우가 서로 같다 해도, $\alpha, \beta$가 커질수록 분산은 매우 작아집니다. $\alpha, \beta$가 커진다는 것은 성공 횟수와 실패 횟수라는 데이터가 그만큼 많이 쌓였다는 것이고, 그에 따라 분산은 감소하는 것으로 볼 수 있을 것 같습니다.


$Reference$