[연속형 분포] 정규 분포(Normal Distribution)와 중심극한정리(Central Limit Theorem)

About Mathematical Statistics

이번 포스트의 주제는 정규 분포(Normal Distribution)입니다. 정규 분포의, 기대값, 분산, 적률생성함수를 구해 보고, 중심극한정리(Central Limit Theorem)에 대해 이해해보고자 합니다.

정규 분포(Normal Distribution)

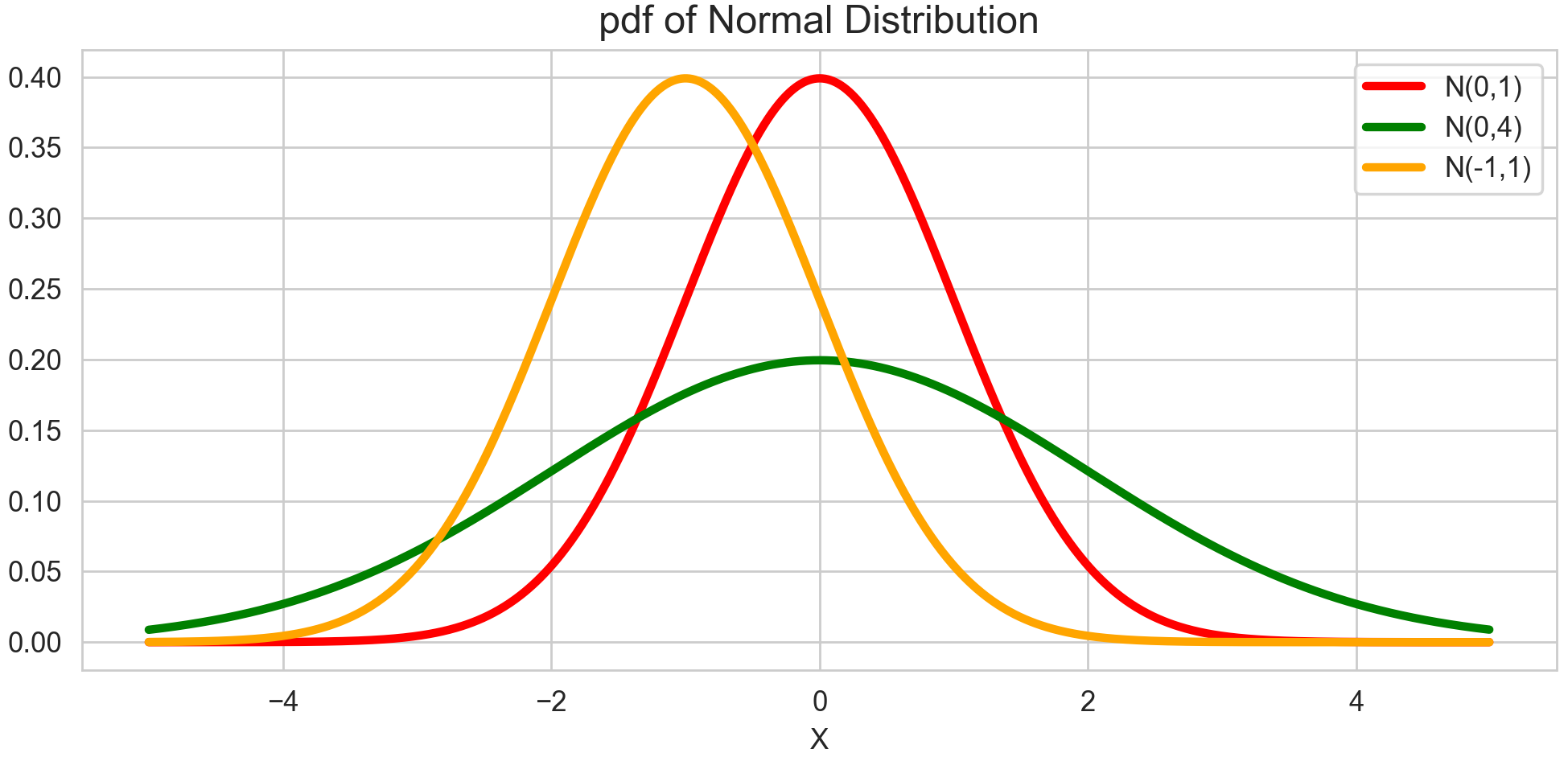
정규 분포, 또는 가우시안 분포(Gaussian Distribution)라고도 불리는 이 분포는 아마 가장 유명한 연속형 확률분포일 것입니다. 가장 쓰임새도 많고, 특히 우리 실생활의 정말 많은 현상이 정규분포를 따르고 있다고 합니다. 예를 들어, 남성의 키, 여성의 키 정규분포를 따르고 있다고 하는데요. 정규분포를 따른다는 건 어떤 의미일까요? 아래 그림과 같이 정규 분포는 가운데 봉우리 하나가 치솟은, 대칭적인 형태를 띄고 있습니다.

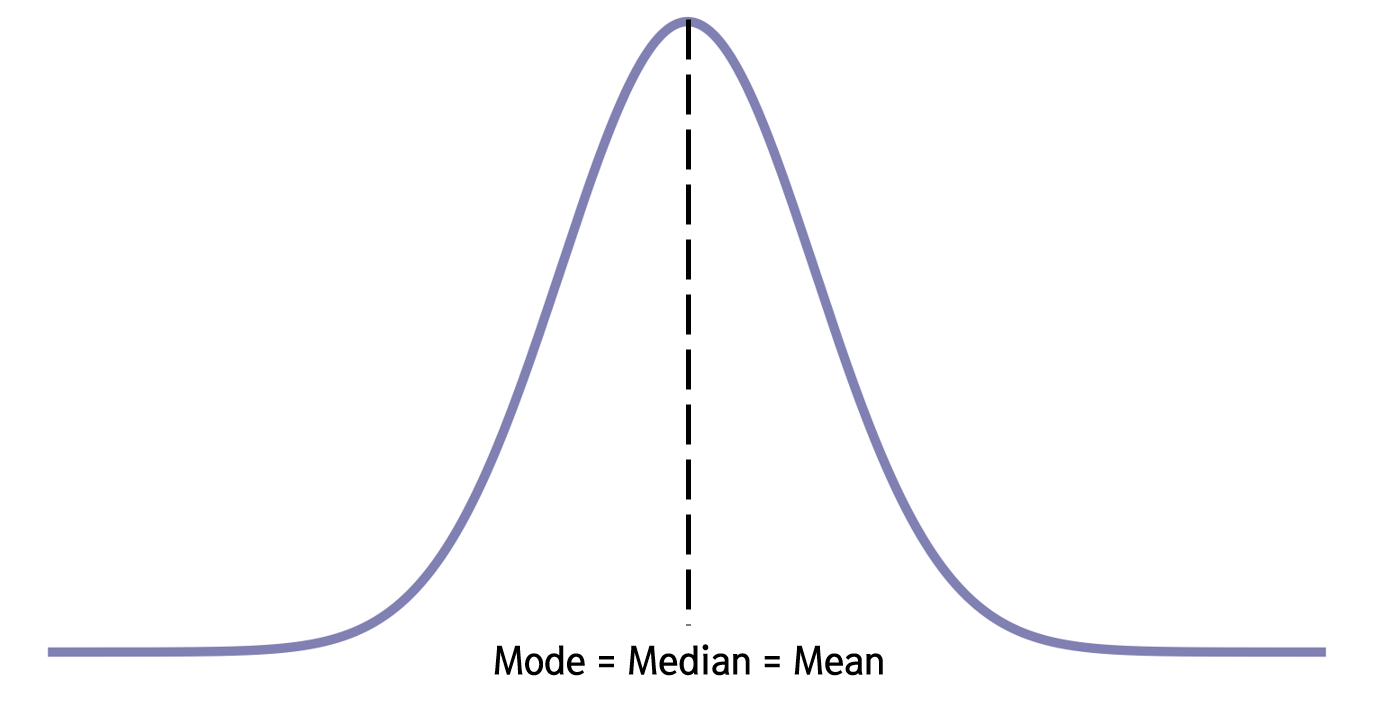
봉우리의 해당하는 부분은 자명하게 최빈값(Mode)일 것이고, 대칭적인 형태이므로 중앙값(Median)에 해당할 것입니다. 한편, 정규분포에서는 이 부분이 바로 평균(Mean)입니다. 즉, 정규분포는 최빈값, 중앙값, 평균이 모두 같다는 특징을 가지고 있습니다. 우리나라 여성들의 키 중 그 빈도가 가장 많은 것이 우리나라 여성 키의 평균이자 중간값이라는 것을 의미할 것입니다. 정확하게 최빈값, 평균, 중간값이 항상 일치하는건 모르겠지만, 비슷한 경우는 뭔가 직관적으로도 우리 실생활에서 많이 볼 수 있을 같다라는 생각이 듭니다.

이제 정규분포의 확률밀도함수를 살펴보겠습니다!

\[\begin{gathered} X \sim N(\mu, \sigma^2) \cr f_X(x\vert \mu,\sigma) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} \cr (-\infty < x < \infty, -\infty < \mu < \infty, \sigma^2>0)\end{gathered}\]

여기서 모수는 평균($\mu$)과 분산($\sigma^2$)입니다. 평균과 분산이 달라짐에 따라 분포의 형태도 달라지게 됩니다. 이 때, 평균이 0, 분산이 1인 정규분포를 표준 정규분포라고 합니다.


그러면 이제 정규분포의 기대값, 분산, 적률생성함수를 구해보겠습니다. 이 때, 계산의 편리함을 위해 표준 정규분포를 가정하고 값을 구해보고자 합니다. 표준 정규분포의 확률변수를 $Z$라고 할 때, 평균이 $\mu$이고, 분산이 $\sigma^2$인 정규분포의 확률변수 $X$는 다음과 같이 표현할 수 있고, 이걸 이용해서 기대값과 분산 및 적률생성함수도 쉽게 구할 수 있기 때문입니다.

\[\begin{gathered} X\sim N(\mu, \sigma^2),\space Z\sim N(0,1) \cr X = \sigma Z +\mu \end{gathered}\]

Z의 적률생성함수, 기대값, 분산을 먼저 구해보겠습니다.

\[\begin{aligned} M_Z(t) &= E(e^{tz}) = \int_{-\infty}^\infty e^{tz} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}z^2} \space dz \cr &=e^{\frac{1}{2}t^2}\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}(z-t)^2} \space dz \cr &= e^{\frac{1}{2}t^2}\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}w^2} \space dw \cr &= e^{\frac{1}{2}t^2}\end{aligned}\] \[\begin{aligned} E(Z) &= M^{(1)}_Z(0) = te^{\frac{1}{2}t^2} \vert_{t=0} =0 \cr E(Z^2) &= M^{(2)}_Z(0) = e^{\frac{1}{2}t^2}+t^2e^{\frac{1}{2}t^2}\space \vert_{t=0}=1 \cr Var(Z) &= E(Z^2) - E(Z)^2 = 1 \end{aligned}\]

이걸 이용해서 $X$의 적률생성함수와 기대값, 분산을 구하면 다음과 같습니다.

\[\begin{aligned} M_X(t) &= E(e^{tX}) = E[e^{t(\sigma Z+\mu)}] \cr &= e^{\mu t} E[e^{t\sigma Z}] = e^{\mu t} e^{\frac{1}{2} \sigma^2 t^2} \cr &= e^{\mu t+\frac{1}{2} \sigma^2 t^2} \cr E(X)&=E(\sigma Z+\mu) =\sigma E(Z)+\mu = \mu \cr Var(X) &= Var(\sigma Z+\mu) = \sigma^2 Var(X) = \sigma^2 \end{aligned}\]


중심극한정리(Central Limit Theorem)

중심극한정리는 제 기억으로 고등학교 수학에서도 배웠던 것 같은데요. 정말 중요하고 유명한 정리인 만큼 중심극한정리에 대해서는 많은 분들이 잘 알고 계실것 같습니다! 중심극한정리는 다음과 같습니다.

Thm. (CLT) $X_1, \cdots, X_n$을 평균이 $\mu$, 분산이 $\sigma^2 (0<\sigma^2 <\infty)$인 모집단에서 추출한 확률 표본이라고 하자. 이 때, $\bar X_n$를 n개의 표본에서 얻은 표본평균이라고 할 때, $n$이 커질수록, $\sqrt n(\bar X_n - \mu)/\sigma$는 표준 정규분포로 수렴한다. \(Z_n = \frac{\sqrt n (\bar X_n -\mu)}{\sigma} \space \rightarrow \space N(0,1)\)

결국 확률변수 $\bar X$는 평균이 $\mu$이고, 분산이 $\frac{\sigma^2}{n}$인 정규분포에 근사하게 된다는 것을 의미합니다. 어떤 모집단에서 샘플을 뽑고, 그 샘플의 표본 평균을 구하는 것을 반복했을 때, 특히 그 샘플 수를 크게 할수록, 구한 표본 평균들은 정규분포를 따른다는 것입니다! 여기서 중요한 것은, 모집단에 대해 특정 분포를 가정할 필요가 없다는 것입니다. 즉, 모집단이 어떠한 분포이든지 간에, 샘플 사이즈가 크다면 표본 평균의 분포는 정규분포에 근사하게 됩니다. 자, 이 정리의 의미를 조금 더 이해해보겠습니다. 우리나라 여성의 키의 분포를 알고싶다고 합시다. 우리나라 전체 여성의 키를 한명도 빼놓지 않고 수집하기는 현실적으로 어려울 것입니다. 그렇다면 전체를 조사할 수는 없어도, 전체를 대표할 수 있는 표본을 충분히 잘 뽑아서 조사하면 그 분포를 추정할 수 있지 않을까요? 이 때, 각 지역별로 여성을 백 명씩 뽑아서 평균을 내고, 평균을 내는 것을 반복해서 많은 평균들을 얻었을 때, 이 평균들은 어떤 분포를 띄게 될 것이고, 위 중심극한정리에 의하면 이 분포가 바로 정규분포에 가깝다는 것입니다! 이 때, 이 표본 평균들의 분포를 표본 분포(Sampling Distirbution)라고 하고, 우리나라 여성의 키의 분포를 모분포(Population Distribution)라고 합니다. 그런데, 위 중심극한정리에서 확인할 수 있듯이, 표본 분포는 모분포의 모수를 기반으로 하는 정규분포$N(\mu, \frac{\sigma^2}{n})$에 근사하게 됩니다. 그렇다면 우리가 구한 표본분포를 이용해서, 알 수가 없었던 모분포의 모수(parameter)를 추정할 수 있게 됩니다! 다시 말해서, 중심극한정리는 표본을 이용해서 모수를 추정하는 근거가 됩니다. 데이터, 즉 우리가 수집한 표본을 이용해서 우리가 알고 싶은 바로 그 “진짜”를 추정하는 (추론)통계학에서 왜 중심극한정리가 그 근간이 되는지 알 수 있는 대목입니다.

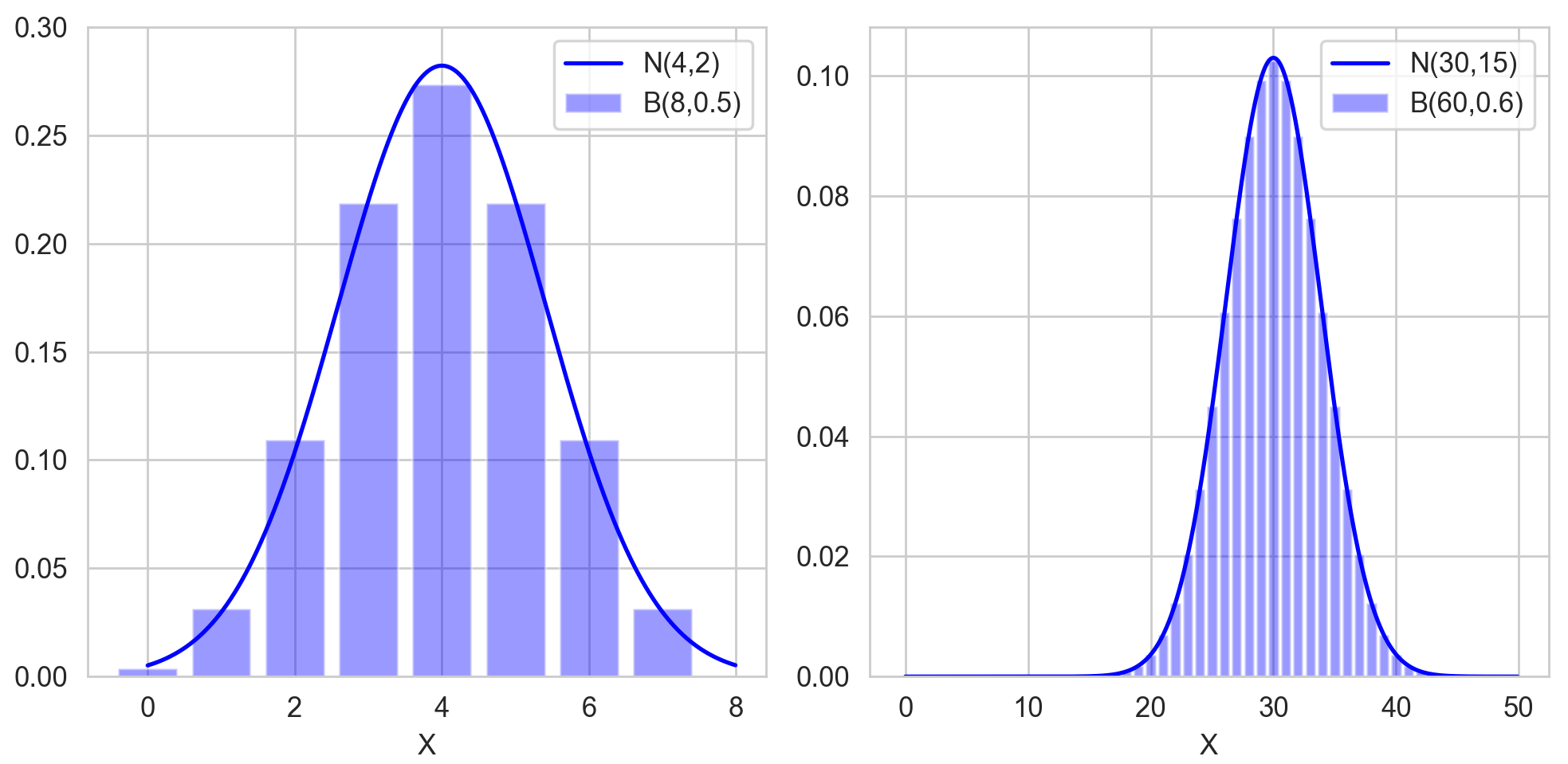
한편, 모분포가 정규분포가 아니어도 된다고 했었는데요. 이에 대한 대표적인 예로, 이항분포가 있습니다. 이항분포는 샘플 사이즈가 충분히 클 때, 정규분포에 근사하는 것을 이용해서 계산을 더욱 간편하게 하곤 하는데요. 샘플 사이즈가 $n$, 성공 확률이 $p$인 이항 분포는 평균이 $np$, 분산이 $np(1-p)$인 정규분포에 근사하게 됩니다.

\[\begin{gathered} Y_n \sim B(n, p) \cr \frac{Y_n - np}{\sqrt {np(1-p)}} \space \rightarrow \space N(0,1) \end{gathered}\]

이 식을 위의 중심극한정리에서 했던 식과 좀 더 유사하게 바꿔볼까요? 확률변수 $X_1, \cdots, X_n$이 성공확률이 $p$인 베르누이 분포, 다른 말로 $n=1$인 이항 분포 $B(1,p)$를 따른다고 하겠습니다. 그러면 평균은 $p$, 분산은 $p(1-p)$가 될 것입니다. 이 때, $Y_n$을 $X_i$들의 합이라고 한다면, $Y_n$이 바로 $B(n,p)$를 따르게 될 것입니다. 즉, 이들의 관계는 다음과 같이 나타낼 수 있게 됩니다.

\[\begin{gathered} X_1, \cdots , X_n \sim B(1,p) \cr Y_n = X_1 + \cdots + X_n \sim B(n,p)\cr \frac{Y_n - np}{\sqrt{np(1-p)}} = \frac{\sqrt n (\bar X_n - p)}{\sqrt{p(1-p)}} \space \rightarrow \space N(0,1) \end{gathered}\]

동전을 반복적으로 던져서 앞면이 나오는 개수를 셀 때, 앞면이 나오는 개수는 전체 개수의 절반을 평균으로 하는 정규분포에 근사하게 된다는 것이고, 무한번 던지게 되면 아예 정규분포를 따른다고 말할 수 있게 되는 것입니다. 한편, 아래 그림에서 왼쪽은 $n=8$인 경우이고, 오른쪽은 $n=60$인 경우입니다. 확실히 샘플 사이즈가 커질수록 이항분포가 정규분포에 더 잘 근사하게 되는 것을 볼 수 있습니다.