[기초통계학] 2편. 가설검정(+p-value, 유의수준 등)에 대한 직관 이해

About Statistics

안녕하세요! 저번 포스트에서는, 통계학의 개요와 통계적 추론의 한 갈래인 추정에 대해서 알아보았는데요. 이번 포스트에서는, 또 다른 갈래인 가설 검정(testing)에 대해 알아보고자 합니다. 통계적 가설 검정할 때 나오는 개념들, 예를 들어 귀무가설, p-value, 유의수준, 1,2종 오류 등등에 대한 직관을 이번 시간에 이해해보도록 하겠습니다👊


가설 검정

가설 검정은, “통계적 근거를 들어서 모수에 대한 가설에 대해 옳고 그름을 판단하는 과정”을 말합니다. 우리가 고등학교 때 확률과 통계 시간에 배우던 One sample Z-test, 또는 두 집단의 평균을 비교하고 싶을 때 이용하는 Two sample t-test 등 이러한 모든게 다 결국 가설 검정에 해당하는 방법론들입니다. 가설을 검정하기 위해서는, 일단 먼저 가설이 필요하겠죠?

귀무가설 vs 대립가설

가설에는 귀무가설(Null Hypothesis)과 대립가설(Alternative Hypothesis)이 있습니다. 연구자는 자신이 주장하는 바를 대립가설($H_a$)로 놓고, 그에 반하는 주장 또는 현재까지 받아들여지고 있는 주장을 귀무가설($H_0$)로 설정합니다. 즉, 연구자는 귀무가설을 기각하고 자신의 주장을 채택시키고자 합니다. 연구자는 “귀무가설이 사실이라면, 이렇게 내가 구한 관측치가 나올 확률이 매우 희박하다. 그러니 귀무가설은 틀렸다.”라며, 귀무가설을 기각하려고 하는 것입니다. 그런데 이 때, 만약 이 확률이 그렇게 희박하지가 않아서 충분한 근거가 되지 못한다면, 연구자는 자신의 주장을 버리고 귀무가설로 돌아가게 됩니다. 귀무가설이 사실이라 채택한다기보다는, 귀무가설이 틀리다고 말할 근거가 없어서 어쩔 수 없이 귀무가설을 받아들이는 것이죠.

p-value

그렇다면, 대체 이 확률이라는게 뭘까요? 이 확률이 바로 p-value(유의확률)입니다! p-value는, “귀무가설 하에서 관측된 사건 이상으로 귀무가설에 반하는 사건이 일어날 확률”을 말합니다. 이 확률이 희박하면 희박할수록, 귀무가설이 틀렸다고 말할 만한 강한 근거가 됩니다. 사실 이렇게 사전적 정의만 보면, 뭔소린지 별로 와닿지가 않습니다..😂 예시를 한번 들어보겠습니다. 어떤 후보자가 시장 선거에 출마하기 전에, 자신에 대한 지지율이 0.3을 넘으면 출마할 계획이라고 해봅시다. 그렇다면 이때 귀무가설과 대립가설은 다음과 같이 세울 수 있을 겁니다.

$H_0:$ 00후보에 대한 참 지지율이 0.3보다 낮다.
$H_a:$ 00후보에 대한 참 지지율이 0.3 이상이다.

여기서 ‘참’이라는 표현을 쓴 건, 모수라는 의미를 강조하기 위함입니다. 즉, 표본을 통해 얻은 지지율이 아니라, 찐 지지율을 말하는 것입니다. 이거에 대한 내용은 저번 포스트에서 한 통계학의 개요를 더 참고해주시면 되겠습니다. 아무튼간에, 이제 가설에 대한 검정을 위해 표본을 통해 관측값을 구해야 할 것입니다. 성인 500명을 추출해서, 이 후보에 대한 지지율을 구했더니 0.38 정도가 나왔다고 해봅시다. 찐 지지율이 0.3 보다 낮다고 할 때, 관측값으로 0.38 또는 그 이상의 값이 나올 확률이 바로 p-value입니다! 이 확률이 희박하다면, 찐 지지율이 0.3보다 낮은게 아닐 가능성이 높아지는 것이죠. 그래서, 지지율이 0.3 이상이라는 결론에 이르고, 00후보는 선거에 출마하고자 하겠죠.

그림으로 한번 나타내봅시다. 먼저 아래 그림처럼, 분포 상에서 0.3을 기준으로 0.38이 비교적 가까이 위치하고 있는 상황이라고 해봅시다. 그러면, 0.38과 그 이상이 나올 확률, 즉 p-value가 커질 것입니다. 이 상황은 지금 귀무가설이 참이라고 할 때, 내가 구한 관측치가 나올 가능성이 충분히 높다는 걸 의미합니다. 즉, 이 경우에는 귀무가설을 기각할 근거가 충분치 않게 됩니다.

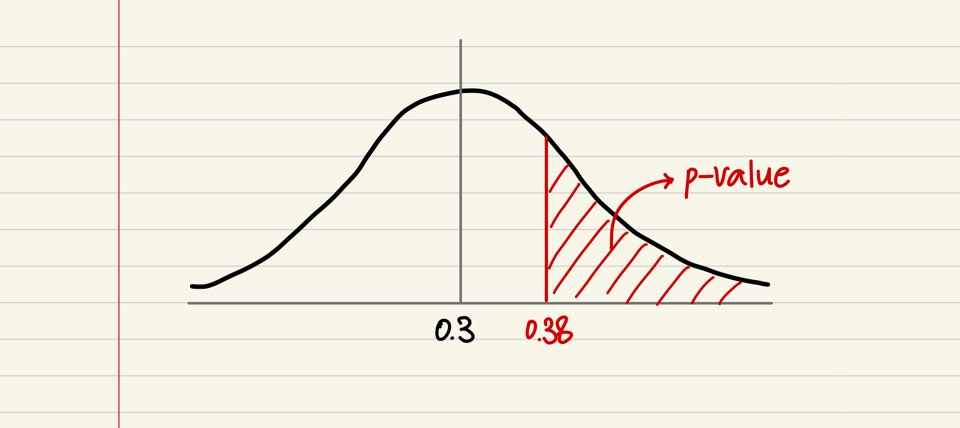p-value가 큰 경우

반면에, 아래 그림처럼 분포 상에서 0.38이 매우 오른쪽 끝에 있다고 해봅시다. 그러면, p-value가 매우 작아질 것입니다. 즉, 해당 분포 하에서는, 내가 나온 관측치가 흔히 나올만한 값이 아니라는 것을 의미합니다. 그러니, 귀무가설이 틀렸을 가능성, 저 분포가 틀렸을 가능성이 높다고 보아, 귀무가설을 기각할 근거가 충분해지는 것입니다.

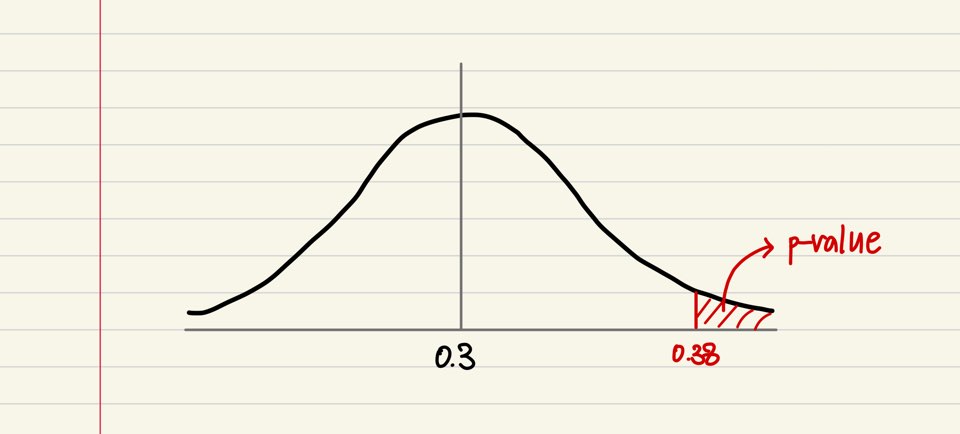p-value가 작은 경우

1,2종 오류

그렇다면 이제, p-value가 ‘작다/크다’ 말할 기준을 세워야 할 것입니다. 그 전에 먼저 1,2종 오류에 대해 짚고 넘어가야 합니다. “귀무가설이 실제로 참인데 이를 기각하는 오류”를 1종 오류라고 하고, 반대로 “귀무가설이 실제로 거짓인데 이를 기각하지 않는 오류”를 2종 오류라고 합니다. 이 두가지 오류를 모두 줄이면 좋겠지만, 두 오류를 동시에 줄이는 것은 불가능합니다. 당연히 기각을 안 할수록, 1종 오류는 감소하고 2종 오류는 증가할 것입니다. 그래서 보통, 1종 오류의 최대 허용치를 설정해놓고, 그 뒤에 2종 오류를 최소화시키는 방식을 선택합니다. 그런데 이 1종 오류의 최대 허용치가 바로 유의수준(Significance level)으로, p-value의 크기를 판단할 기준점이 됩니다! 유의수준은 보통 $\alpha$로 표기하고, 2종 오류의 확률은 $\beta$로 표기합니다.

1,2종 오류

유의수준

p-value가 1종 오류 확률의 최대 허용치, 즉 유의수준($\alpha$)보다 작으면 귀무가설을 기각하고, “유의수준 $\alpha$ 하에서 (통계적으로) 유의하다”고 말합니다. 반대로, p-value가 유의수준보다 크면 귀무가설을 기각하지 않고, “유의수준 $\alpha$ 하에서 유의하지 않다”고 말합니다. 보통 유의수준은 1%,5%의 작은 값으로 고정합니다. 유의수준을 5%로 고정한다는 것은, “100번 중 최대 5번까지 1종 오류가 나타날 수 있다”는 것을 의미합니다.

  • $p-value < \alpha :$ 귀무가설 기각 (Reject $H_0$), $\alpha$ 하에서 유의하다.

  • $p-value > \alpha :$ 귀무가설 기각X (Not Reject $H_0$), $\alpha$ 하에서 유의하지 않다.

그런데 왜 이렇게 1종 오류의 최대 허용 확률을 p-value의 기준점으로, 그것도 이렇게 작은 값으로 고정을 해놓는걸까요? 앞서, 연구자는 귀무가설을 기각하는게 목표라는 것을 기억하시나요? 이 때, 유의수준이 40% 정도로 크다면, p-value가 0.4보다만 작으면 되기 때문에 귀무가설을 기각하기가 매우 쉬워집니다. 즉, 귀무가설이 참이라고 가정했을 때, 관측치가 나올 확률이 그렇게 희박하지 않는데도 귀무가설을 기각하게 되는 것이죠. 다시 말해서, 귀무가설에 그렇게까지 반하는 증거가 아닌데도 귀무가설을 기각하게 되는 것이고, 이렇게 되면 문제점은, 그렇게 해서 얻은 결론에 대한 설득력도 없어진다는 겁니다! 따라서, 유의수준을 일정 수준 이하로 통제하지 않으면, 연구자의 가설에 대한 지지가 설득력을 가질 수 없게 됩니다. 반면에, 유의수준이 굉장히 작다고 해봅시다. 예를 들어, 0.1%라고 한다면, p-value가 0.001보다 작아야 귀무가설이 기각되는 것입니다. 이 경우에는 귀무가설을 기각하기가 굉장히 어려워질 것입니다. 이렇게, 유의수준이 굉장히 낮아 귀무가설을 기각하기 힘든 상황을 “보수적이다“라고 말하기도 합니다.


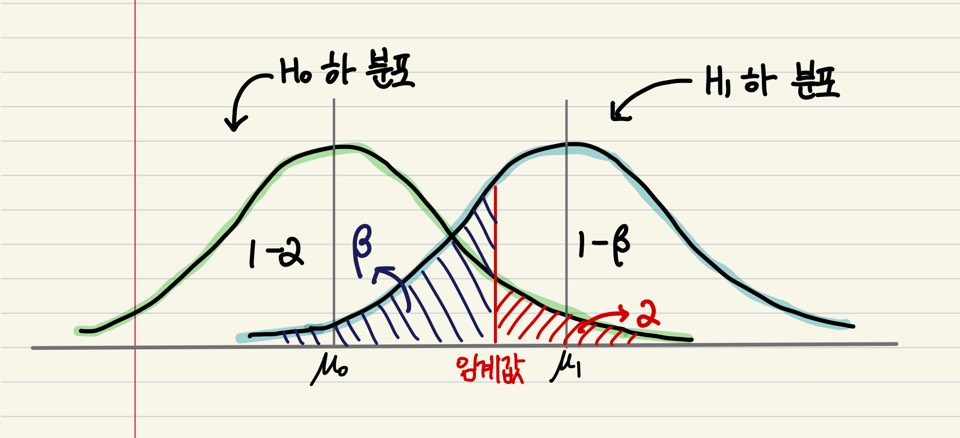
자, 그럼 이제 그림과 함께 정리해보겠습니다. 임계값(Critical value)이라는 것은, 그 이상의 확률이 $\alpha$가 되는 자리값을 의미합니다. 즉, 임계값부터 시작하여 극단적인 방향으로 끝까지의 확률이 바로 유의수준입니다. 아래 그림처럼, 귀무가설이 참이라는 가정 하에서 임계값보다 클 확률이 바로 유의수준이 됩니다. 귀무가설이 사실인데, 임계값보다 커서 귀무가설을 기각하는 경우에 해당합니다. 반대로 대립가설 하에서의 분포에서, 임계값보다 작은 부분의 확률이 바로 2종 오류의 확률인 $\beta$가 됩니다. 즉, 귀무가설이 참이 아닌데, 임계값보다 작아서 귀무가설을 기각하지 않는 경우에 해당합니다. 한편, $1-\beta$ 부분, 즉 귀무가설이 참이 아닌데 기각을 제대로 한 확률을 검정력(power)이라고 부릅니다. 검정력은 크면 클수록 좋습니다.

예를 들어, 다음과 같이 두 분포 모두 분산이 작고 봉우리가 치솟은 형태라면 검정력이 더 증가할 것입니다. 직관적으로도 분산이 크지 않은 분포라는 것은 모호함이 적고 어느정도 이상 설명력이 있는 분포이기에 확실성이 높아진달까요. 그나저나 그림을 너무 못그렸네요ㅎㅎ🤪

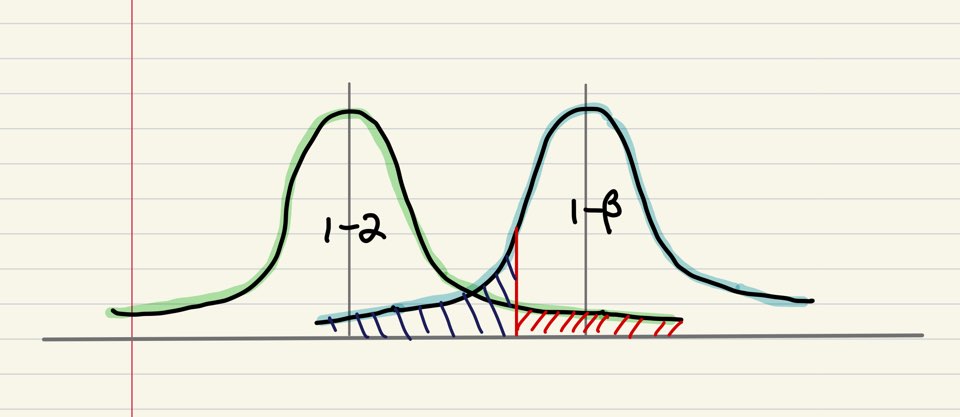검정력의 증가

반대로, 아래 그림처럼 넓게 분포하고 봉우리가 낮은 형태라면 검정력은 감소하겠죠!

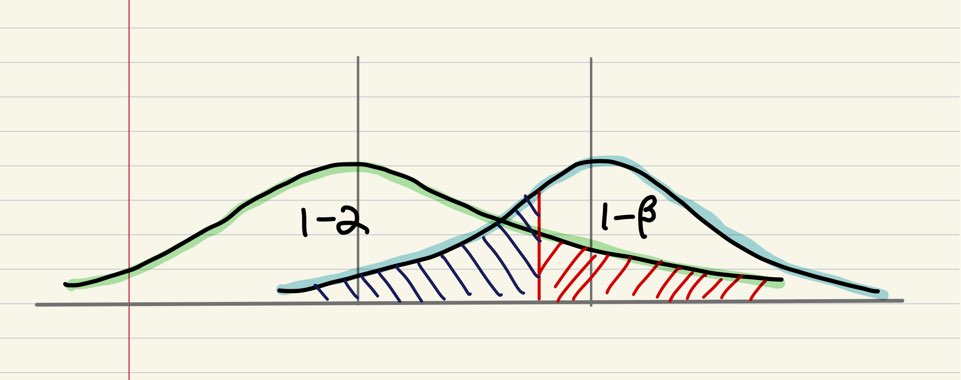검정력의 감소



자, 여기까지 기초 통계학 시리즈의 두번째 포스트를 마쳤습니다! 가설 검정에서 하는 개념들이 조금 이해가 되셨나요? 다음부터는 통계학 수업에서 배우는 방법론들도 포스팅하려고 하는데요. 그 때는 모두 이러한 내용들을 염두에 두고, 분석 결과를 해석하게 될 예정입니다:) 감사합니다!


$Reference$

  • 통계적 탐구, 김기영$\cdot$박유성$\cdot$송석헌$\cdot$이재원$\cdot$장인식$\cdot$전명식$\cdot$허명회, 교우사, 2002

  • 생명과학 연구를 위한 통계적 방법, 이재원$\cdot$박미라$\cdot$유한나, 자유 아카데미, 2005