[회귀분석] 1편. 선형 회귀 개요 및 직관 이해

About Statistics

머신러닝의 해석 시리즈에서는 Black-box 모델들의 결과에 대하여 해석을 할 수 있는 여러가지 방법들을 다루고 있습니다. 그런데, 모델의 해석이라는 분야에서 빠질 수 없는 것들이 아무래도 Simple, Linear 모델들입니다. Black-box 모델들과는 다르게, 구조가 단순하여 모델 output을 직관적으로 해석가능하다는 장점이 있는 모델들이죠! 그래서 앞으로 회귀분석 시리즈에서는, 선형 회귀, 로지스틱 회귀 등 선형 모형의 범주에 속하는 단순한 모형들에 대해 다루고자 합니다. 역시나 목적은 직관을 이해하여 써먹는 것이구요. 이번 포스트에서는 먼저 선형 회귀의 개요 및 직관을 이해해보려고 합니다. 회귀분석의 개요를 설명하는 것에 있어서, 이 글의 도움을 많이 받았습니다! 그럼 시작하겠습니다👊


선형 회귀 개요

“선형” 회귀의 정의

회귀분석이란, 관심대상 $Y$와 $Y$를 설명할 만한 조건/정보들 $X_1,\cdots,X_p$의 함수적 관계 $f(\cdot)$를 찾는 것입니다! 그런데 아래 식에서 우리가 찾고자 하는 $f(\cdot)$ 뒤에 $\varepsilon$이 추가되어 있죠? 이건 오차항, 자연적으로 발생하는 잡음을 의미합니다. 이 친구는 우리가 찾고자 하는 함수적 관계와는 관련이 없지만, 이 친구에 대한 가정이 또 회귀분석에서 매우 중요합니다. 이건 이따가 살펴보도록 하구요. 돌아와서, $f(\cdot)$가 선형(linear) 함수일 경우가 바로 선형 회귀입니다!

\[Y = f(X_1 , \cdots , X_p) + \varepsilon\]

아래와 같이 생긴 모형이 바로 우리가 흔히 보는 선형 회귀입니다! 엄밀하게는, $Y$와 $X_1,\cdots,X_p$의 관계가 선형인 것을 선형 회귀라고 하는 것이 아니라, 회귀계수 또는 회귀모수라고 불리는 $\beta_1,\cdots,\beta_p$와 $Y$의 관계가 선형인 경우를 선형 회귀라고 합니다.

\[Y =\beta_0+\beta_1X_1+\cdots +\beta_pX_p + \varepsilon\]

$X_1,\cdots,X_p$는 저희에게 주어진 데이터죠? 얘네들은 얼마든지 저희가 변환할 수가 있습니다. 예를 들어, $X_1$의 분포가 굉장히 치우친(skewed) 형태라면, 정규분포스럽게 만들어줄려고 $X_1’=log(X_1)$해서 사용하기도 합니다. 이런 식으로 $X_1,\cdots,X_p$을 어떻게든 변수 변환해서, $Y$와 회귀계수들 $\beta_1,\cdots,\beta_p$이 선형적인 관계에 놓여있게 된다면, 선형 회귀가 됩니다!


선형 회귀의 의미

선형 회귀의 정의를 이제 알았는데요. 그럼 좀 더 의미를 이해해보도록 하겠습니다! 선형 회귀를 한 줄로 설명하면 다음과 같습니다.

관심 대상을 설명할 만한 조건/정보들이 주어졌을 때, 관심 대상에 대한 이들의 영향력(가중치)을 추정하여, 특정 조건 하에서 관심 대상의 평균을 구하는 것.

  • 관심 대상: $Y$

  • 조건/정보: $X_1,\cdots,X_p$

  • 영향력(가중치): $\beta_1,\cdots,\beta_p$

  • 특정 조건 하에서 관심 대상의 평균: $ E(Y \vert X_1=x_1, \cdots, X_p=x_p,\ \beta_1,\cdots,\beta_p)$

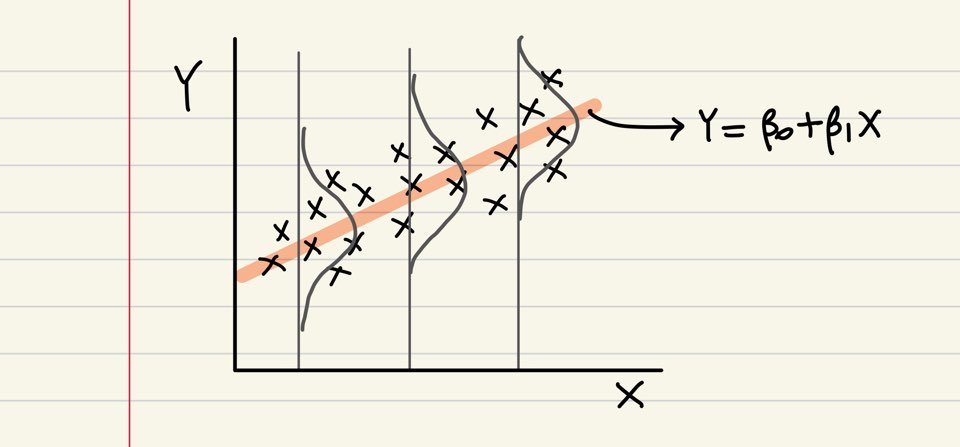선형 회귀: 각 X에서의 Y 평균을 구하는 것

결국 회귀분석은 조건부 평균을 구하는 것입니다! 예를 들어, $Y$는 연봉이고, $X_1$은 성별(0:여성, 1:남성), $X_2$는 직급(0~5)이라고 해보겠습니다. 아래와 같이 제 마음대로 회귀계수들도 적어보겠습니다. 사람마다 연봉의 차이는 정말 천차만별이겠지만, 선형 회귀를 이용하면 어느정도 한정(limit)하고 단순화하여, ‘성별에 따라, 직급에 따라 평균 연봉이 이렇더라’고 말할 수 있습니다.

\[Annual\ Salary = 2000 + 200 \cdot Sex + 1000 \cdot Rank\]

위의 선형 회귀 모형을 해석해볼까요? 단위가 만원이라고 해보면, 같은 직급일 때 남성($Sex=1$)이 여성($Sex=0$)보다 평균 연봉이 200만원 더 높다고 해석할 수 있겠습니다. 직급은 0부터 5까지로 한정해보았는데요. 같은 성별일 때 직급이 하나 올라갈수록 평균 연봉이 1000만원씩 증가한다고 해석할 수 있습니다. 또 한, 연봉에 더 큰 영향을 주는 것은 성별보다는 직급이다 요렇게 볼 수도 있겠네요. 해석이 굉장히 직관적이지 않나요? 선형 회귀는, 각 조건들과 이들의 가중치들로 선형 결합된 수학식이기 때문에, 가중치를 통해 해석하는 것이 굉장히 쉽고 직관적이라는 장점이 있습니다.

한편, 남성($Sex=1$)이고, 직급이 1인($rank=1$)인 그룹 내에서도 연봉은 또 차이가 있을 것입니다. 그 차이가 작을 수도 있고, 클 수도 있고, 아니면 대부분은 어느정도 값인데 연봉이 혼자 무지막지하게 높은 사람이 있을 수도 있을 것입니다. 회귀 분석에서는, 각 개체의 연봉이 평균 연봉을 중심으로 일종의 랜덤하고 동일한 오차들이 부여된 형태라고 가정합니다! 이것이 앞에서 살짝 언급했던 오차항에 대한 가정입니다.

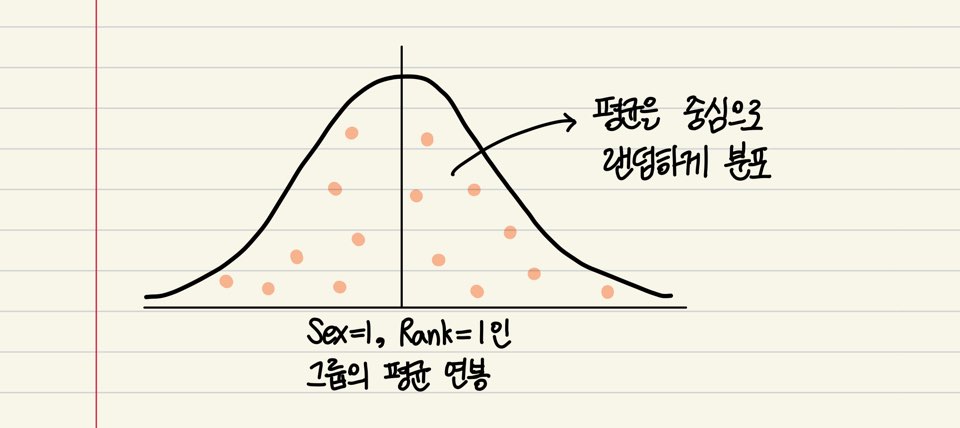랜덤하고 동일한 오차


오차항에 대한 가정과 진단의 필요성

우리가 찾고자 하는 패턴과 상관 없는, 자연적인 오차는 생기기 마련입니다. 각 개체에 내포되어 있는 이러한 오차항 $\varepsilon_1, \cdots, \varepsilon_n$은 평균이 0이고 분산이 일정한 정규분포를 따르며 서로 독립이라고 가정합니다.

\[y_i =\beta_0+\beta_1X_{i1}+\cdots +\beta_pX_{ip} + \varepsilon_i, \quad (i=1,\cdots,n)\]

즉, 오차항의 정규성, 등분산성, 독립성 가정은 선형 회귀 모형의 필수 가정으로, 모델 적합 후에 가정 위반 여부를 진단해야 합니다. 왜 그럴까요? 오차항이 이러한 가정을 위반하게 되면, 평균이 대표값 역할을 충분히 하지 못하는 경우가 많을 것입니다. 앞서 언급했듯이, 혼자 무지막지한 연봉을 받는 한 사람이 존재하면, 전체 평균이 올라갈 것이고 이는 의미있는 대표값으로 보기 어렵습니다. 또 한, 특정 조건에 따라 오차항들의 편차가 상이하거나, 랜덤하지 않고 패턴을 보일 경우에도 마찬가지입니다. 직급이 올라갈수록 연봉의 편차가 너무 심하게 커질 경우, 이는 등분산성 가정을 위반하는 사례입니다. 오차항이 순서에 따라 패턴을 보일 경우, 예를 들면 시간에 따른 주식 데이터는 오차항의 독립성을 위반하는 대표적인 사례입니다. 그렇기 때문에 선형 회귀의 경우, 모델을 적합시키고나면 회귀 진단(Diagnosis)을 해야 합니다. 회귀 진단은 아마 3편? 정도에서 다룰 것 같습니다!

선형 회귀 모형은, 오차항에 대한 가정 외에도 추가적으로 '모형이 선형적이어야 한다', '예측변수들 간 선형 종속이 아니다' 등등의 몇가지 가정을 베이스로 두고 있습니다. 구조가 굉장히 단순한 만큼 제약 조건이 참 많습니다😂 만약 이러한 가정들이 위반되었을 때, 선형 회귀를 무조건 사용할 수 없는 것은 아니고, 어느정도 대처할 수 있는 방안들도 존재합니다! 앞서 잠깐 언급했던 변수 변환(Variable Transformation)도 가정 위반을 완화하기 위해 많이 사용됩니다. 심하게 튀는 값들의 영향을 덜 받기 위해 가중치가 부여된 더 로버스트한 회귀를 이용할 수도 있구요. 여러가지 방안들을 시도했음에도 가정 위반이 해결되지 않을 경우에는, 다른 모델을 사용하는 편이 더 적절하다고 볼 수 있을 것 같습니다.



선형 회귀의 개요만 다뤘는데도 글이 꽤 길어졌네요! 다음 포스트에서는, R이나 Python으로 선형 회귀를 돌리면 나오는 output을 이해하기 위한 개념들을 살펴보려고 합니다. 선형 회귀에서의 모수 추정, 개별 회귀계수의 유의성 검정, 모델의 적합도 검정 등에 대해 이해한 뒤, R/Python으로 돌려보는 것까지 진행해보겠습니다. 감사합니다:)


$Reference$

  • https://brunch.co.kr/@gimmesilver/64

  • Regression Analysis by Example 5th edition, Samprit Chatterjee $\cdot$ Ali S. Hadi, 2015