[회귀분석] 2편. 선형회귀 output에 나오는 개념 완벽 이해 (in R/Python)

About Statistics

안녕하세요, 회귀분석 시리즈 2탄입니다! R이나 Python으로 선형 회귀 적합 후에 확인할 수 있는 output을 어떻게 해석하고 이해하면 되는지 이번 포스트에서 알아보려고 합니다. R에서는 선형 회귀를 적합하게 되면, 다음과 같은 아웃풋이 나오구요.

R에서의 선형 회귀

Python에서는 statsmodels.formula.api 패키지를 이용해서 다음과 같은 아웃풋 창을 얻을 수 있습니다.

Python에서의 선형 회귀

두 프로그램 모두 공통된 통계량이 나와있는 걸 확인할 수가 있는데요. 회귀계수 추정치와 관련해서는, t-value, p-value 등등이 나와있고, 그 외에도 Multiple R-squared, Adjusted R-squared, F-statistic 등등이 나와있네요. 그러면, 이러한 통계량들의 이론적 배경을 살짝 살펴보면서 어떤 의미를 가진 통계량인지 알아보겠습니다! 개념들을 모두 파악한 후에, R과 Python으로 선형 회귀를 적합해보겠습니다. 코드가 궁금하신 분들은 바로 맨 아래로 이동하시면 됩니다😃


회귀계수의 추정, 검정, 해석

회귀계수 추정

가장 먼저 모델을 구성하는 회귀계수들이 어떻게 해서 추정된 건지 알아봐야겠죠? 회귀계수들은 최소제곱법(Least Squares Method)을 이용해서 추정되었습니다! 최소제곱법은, 각 점으로부터 구하고자 하는 최적 직선까지의 수직 거리(잔차)의 합을 최소화하는 직선 방정식을 제공합니다. 아래 그림처럼, 수직 거리의 제곱합을 최소화하는 것이기 때문에, 아래 오른쪽 그림처럼 사각형들의 합을 최소화하는 직선을 찾는다고 이해할 수 있겠네요.

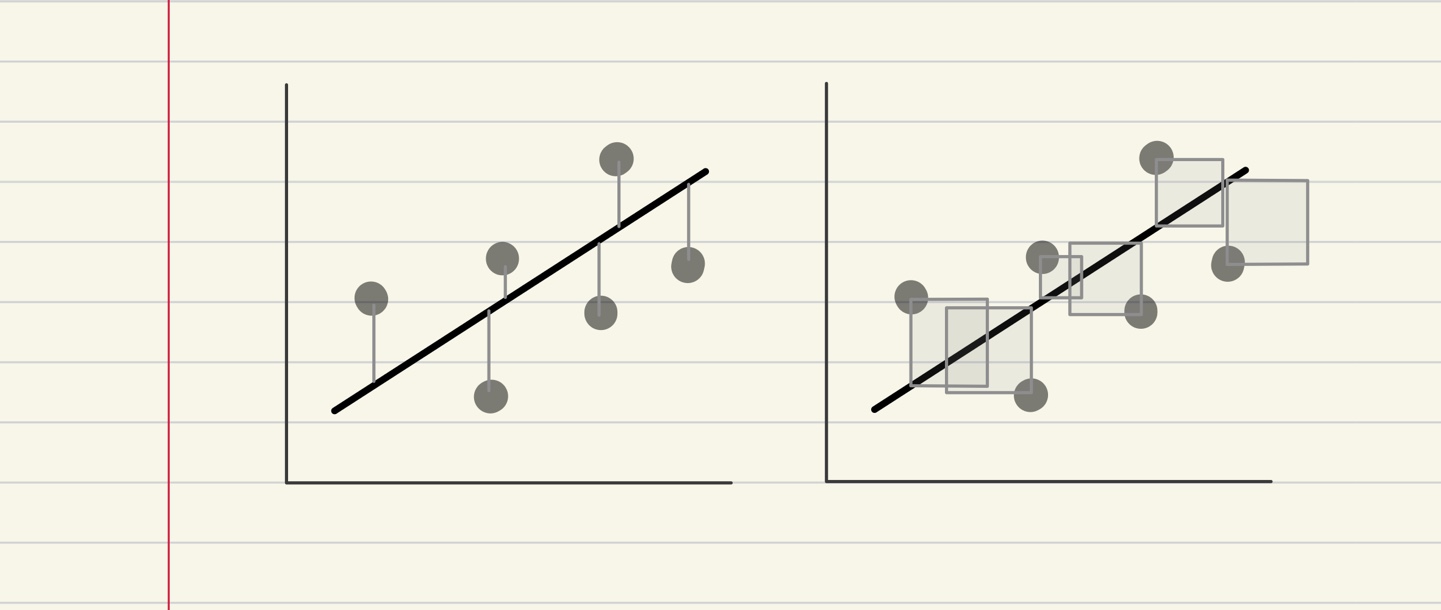최소제곱법

변수 개수가 $p$개 이고, 전체 샘플 개수가 $n$개인 데이터에 대해, $i$번째 샘플에 대한 회귀 모델이 다음과 세워진다고 해보겠습니다. $(i=1,\cdots,n)$ 그러면, $y_i$를 뒤로 빼서 $\varepsilon_i$에 대해 나타낼 수 있습니다.

\[y_i = \beta_0X_{i1}+\cdots + \beta_pX_{ip} + \varepsilon_i,\quad \varepsilon_i \overset{iid}\sim N(0,\sigma^2)\] \[\varepsilon_i=y_i - \beta_0X_{i1}+\cdots + \beta_pX_{ip}\]

아래 그림과 같이 잔차 제곱합을 최소화하는 모수를 추정하는 것이기 때문에, 잔차제곱합을 미분하여 0이 되게 하는 지점을 찾는 것으로 회귀계수($\hat \beta_0, \cdots, \hat \beta_p$)를 추정합니다. (그림과 같이 아래로 볼록한 함수일 때) 미분하여 0이 되는 지점이 잔차제곱합에서 최소점에 해당하기 때문입니다.

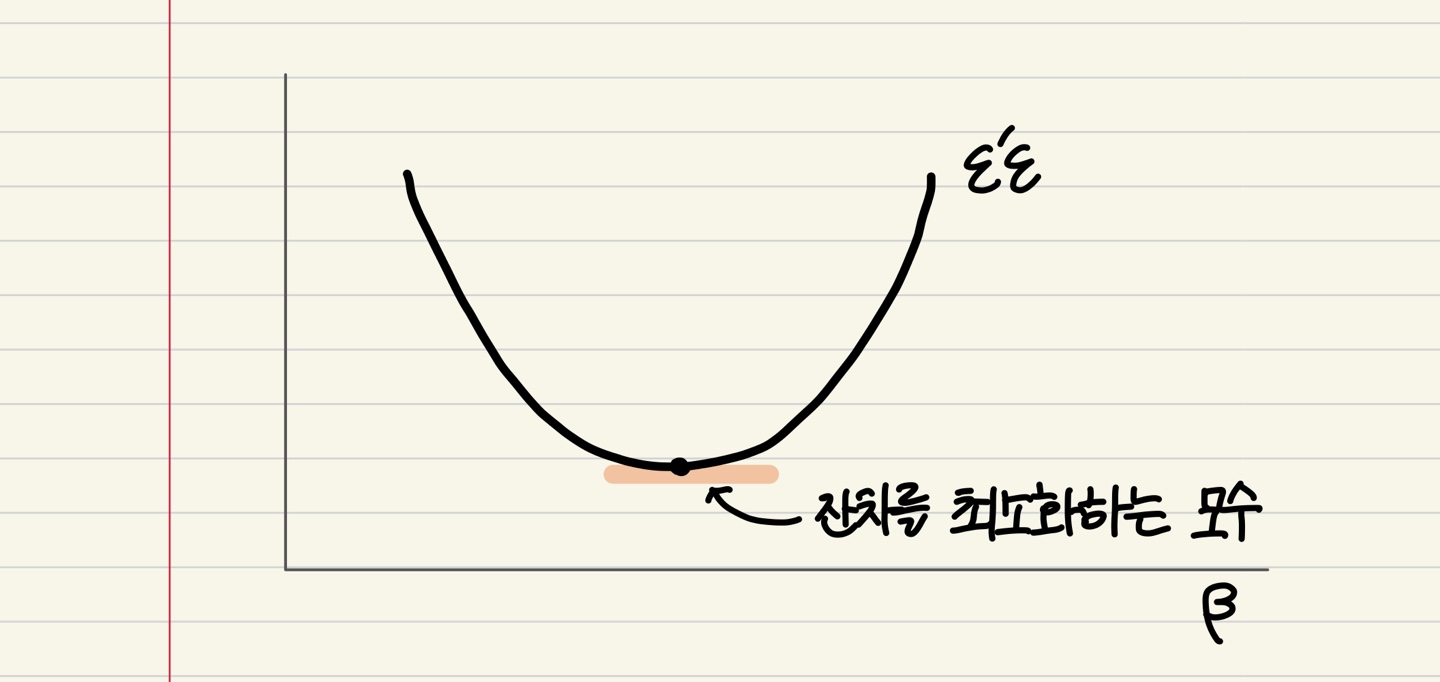잔차제곱합의 최소화 지점

\[S(\beta_0,\beta_1,\cdots,\beta_p) = \sum^n_{i=1}\varepsilon_i^2 = \sum^n_{i=1}(y_i - \beta_0x_{i1}+\cdots + \beta_px_{ip})^2\] \[\frac{\partial}{\partial \beta0} S(\beta_0,\beta_1,\cdots,\beta_p) \overset{set}= 0 \implies \hat\beta_0\] \[\frac{\partial}{\partial \beta1} S(\beta_0,\beta_1,\cdots,\beta_p) \overset{set}= 0 \implies \hat\beta_1\] \[\vdots\]

회귀계수 해석

자, 이렇게 구한 회귀계수는 다음과 같이 해석합니다.

  • $\beta_0:$ $X_1=\cdots=X_p=0$일 때 $Y$의 기대값.

  • $\beta_j:$ $X_j$를 제외한 나머지 모든 예측 변수들을 상수로 고정시킨 상태에서, $X_j$의 한 단위 증가에 따른 $Y$의 증가분. 또는, 다른 예측변수들에 의하여 $Y$와 $X_j$가 조정된 후, 반응 변수 $Y$에 대한 $X_j$의 공헌도.

즉, $X_j$에 대한 회귀계수 $\beta_j$는, 다른 모든 변수들은 고정한 채, $X_j$를 한 단위 증가시켰을 때 $Y$의 증가하는 정도(partial effect)를 의미합니다! 이러한 점에서, 선형 회귀에서는 변수들 간 연관성이 너무 심하면 안된다는 것을 짐작할 수 있습니다. 변수들 간 연관성이 너무 심하게 되면, 다른 변수들은 고정하고 난 그 변수만의 영향력이라고 보기 어렵게 되기 때문입니다.

회귀계수 유의성 검정

선형 회귀 적합 결과에서 회귀계수 추정치 옆에 제시되는 또 다른 중요한 것이 바로 회귀계수에 대한 유의성 검정과 관련된 통계량입니다! 회귀계수에 대해 유의성 검정은, 해당 변수가 Y에 유의한 영향을 끼치는 변수인지 통계적인 근거로 결론을 내리는 과정입니다. 검정이 생소하신 분들은 [기초통계학] 2편. 가설검정(+p-value, 유의수준 등)에 대한 직관 이해를 참고하시면 될 것 같습니다:) 변수 $X_j$에 대한 회귀계수의 유의성 검정을 위한 귀무가설과 대립가설은 먼저 다음과 같습니다.

\[H_0: \beta_j = 0 \quad vs \quad H_1: \beta_j\not = 0\]

즉, 귀무가설은 “($Y$에 끼치는) 변수 $X_j$의 영향이 없다.”이고, 대립가설은 “영향이 있다.”가 됩니다. 이 검정에 대한 통계량은 다음과 같습니다.

\[t_j = \frac{\hat \beta_j}{s.e(\hat \beta_j)} \quad \sim t_{(n-p-1)}\]

이 때, p-value가 0.05보다 작다면, 귀무가설을 기각하고 “변수 $X_j$는 유의수준 5% 하에서 $Y$에 유의한 영향을 끼친다”고 결론내릴 수 있습니다. 95% 신뢰구간은 다음과 같이 계산이 되는데요. 95% 신뢰구간이 만약 0을 포함하지 않으면, 마찬가지로 유의수준 5% 하에서 귀무가설을 기각할 수 있습니다.

\[95\% \ C.I: \hat \beta_j \pm t_{(n-p-1, \alpha/2)}\times s.e(\hat \beta_j)\]

모델 적합도

지금까지 회귀계수의 추정, 해석, 검정까지 모두 살펴보았습니다. 이번에는, 개별 회귀계수에 대한 것이 아니라, 전체 모델의 적합도가 어느정도인지 나타내는 통계량들을 알아보려고 합니다! 일단, 회귀계수들을 추정하여 적합한 회귀 모델 $\hat y_i$는 다음과 같이 나타낼 수 있습니다.

\[\hat y_i = \hat\beta_0 + \hat\beta_1 x_{i1} +\cdots + \hat\beta_p x_{ip}\]

그러면, 이 모델이 좋다고 할 수 있을지 아닌지 통계적으로 파악해봅시다! 먼저, 모델의 적합도를 평가하는 가장 유명한 척도에는 $R^2, R^2_{adj}$가 있습니다.

다중 상관계수: $R^2, R^2_{adj}$

$\sum (y_i - \bar y)^2$는 $Y$의 전체 변동(Variance)을 나타냅니다. 여기서 $\bar y$는 $y$의 표본평균을 의미하는데요. 왜 하필 평균일까요? 평균은, 아무 변수들도 주어지지 않았을 때 y를 설명하기 위한 최선책이 됩니다. 즉, 아무런 정보가 주어지지 않았을 때, 표본평균이 그나마 $y$를 가장 잘 설명하는 통계량이 되는 것이죠. 그래서, 우리가 모델의 적합도를 평가할 때 이용하는 아이디어는, 표본평균보다 내 모델이 확실히 $y$를 더 많이 설명한다고 할 수 있냐는 것입니다! 표본 평균보다는 더 많이 설명해야 하는게 확실한데, 그 정도가 미미하면 적합도가 그리 좋지 않다고 보는 것입니다. 다중 상관계수 $R^2$의 아이디어는 이러한데, 어떻게 계산되는지 좀 더 들여다 보겠습니다.

$y$의 전체 변동은 두개의 서로 다른 특성을 가진 제곱합 $\sum (\hat y_i -\bar y)^2, \sum (y_i - \hat y_i)^2$으로 쪼개질 수 있습니다. 전자는 적합값과 $y$의 전체 평균의 차이에 대한 제곱합인데, 이 제곱합은 (전체 평균에 비해) 모델에 의해 더 설명되는 변동을 의미합니다! 반면, 후자는 실제 $y_i$와 적합값 $\hat y_i$의 차이에 대한 제곱합으로, 모델에 의해 설명되지 않는 변동을 의미합니다. 전자는 SSR(Sum of Squares Regression), 후자는 SSE(Sum of Squares Error)로 보통 줄여서 지칭하기도 합니다.

그림으로 보면 좀 더 잘 이해가 되실 것 같은데요! 모델에 의해 설명되지 않는 부분(SSE)을 줄이면, 모델에 의해 설명되는 부분(SSR)이 증가하고, 이 경우 모델의 적합도는 매우 높다고 볼 수 있습니다.

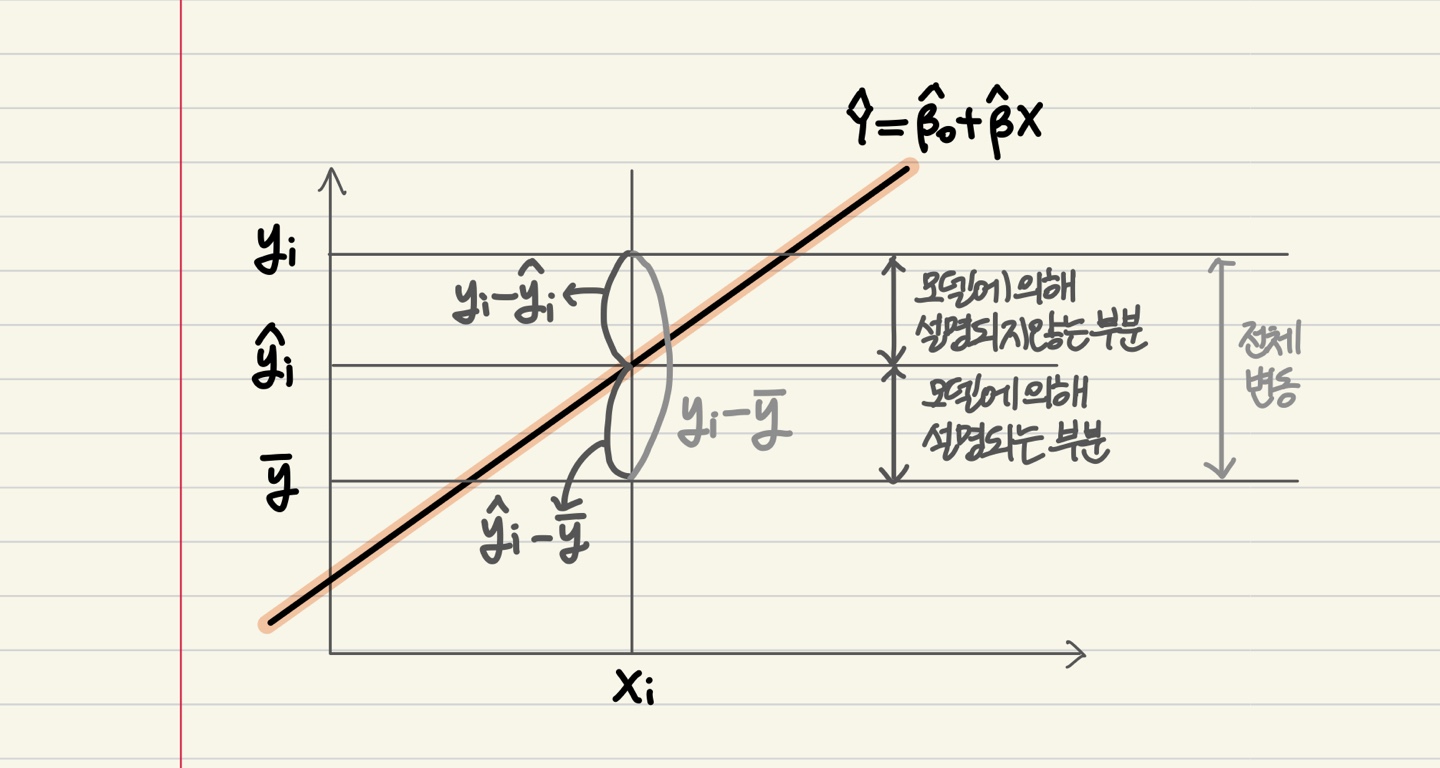
$R^2$는 결국 전체 변동(SST) 대비 모델이 설명하는 변동(SSR)의 비율을 의미합니다! SSR은 SST보다 클 리는 없기 때문에, 비는 0과 1사이가 됩니다.

\[R^2 = \frac{SSR}{SST} = 1- \frac{SSE}{SST} \quad (0 \le R^2 \le 1)\]

자자, 그런데 변수 개수가 많아지면 많아질수록, $R^2$는 커지게 됩니다. 그렇기 때문에, 변수 개수를 보정한 $R^2$가 필요하게 되었고, 이것이 바로 $R^2{adj}$ 입니다! $R^2{adj}$ 는 변수 개수가 서로 다른 회귀 모델의 적합도를 비교할 때 유용합니다.

\[R^2_{adj} = 1-\frac{SSE/(n-p-1)}{SST/(n-1)}\]

모델 유의성 검정: $F-statistic$

$R^2$는 보통 우리가 참고를 하는 척도이고, 모델이 유의하다 아니다 결론을 내릴 수 있는 특정한 기준은 없습니다. 또 결론을 내리고 싶으면 이제 검정을 해야겠죠? 회귀계수의 유의성을 검정하는 것과 마찬가지로, 모델의 유의성도 검정할 수가 있습니다. 이 때, 귀무가설과 대립가설은 다음과 같습니다!

\[H_0: \beta_1=\cdots = \beta_p =0 \quad vs \quad H_1: not\ H_0\]

회귀계수들이 모두 0이다.. 무슨 뜻일까요? 즉, 귀무가설은 변수들을 아무것도 포함하지 않은, 절편항만 존재하는 모델이 참이라는 겁니다. 때문에, 귀무가설은 이렇게도 쓸 수가 있습니다.

\[H_0: Y=\beta_0+\varepsilon \quad vs \quad H_1: Y=\beta_0+\beta_1X_1+\cdots +\beta_pX_p +\varepsilon\]

이러한 귀무가설을 가지고 검정을 한다는 것의 의미는 또 무엇일까요? 내가 포함한 변수들이 효과가 없다고 가정할 때, 그 변수들을 포함하여 적합한 회귀모델이 설명하는 정도가 그만큼 또는 그 이상 나올 확률이 희박한지 아닌지 검정하는 것입니다. 그 확률이 이제 희박하면, 내가 포함한 변수들이 효과가 없는게 아니라고, 즉 귀무가설이 틀렸다고 볼 수 있는 것이죠! 이 부분은 [기초통계학] 2편. 가설검정(+p-value, 유의수준 등)에 대한 직관 이해를 더 참고해주세요..ㅎㅎ 결국 그냥 귀무가설을 기각하면 “적합한 모델이 유의수준 $\alpha$%하에서 유의하다” 이렇게 결론내릴 수 있습니다. 이 때의 통계량 $F$는 바로 위에서 했던 SSR, SST 또는 $R^2$를 이용해서 구할 수 있습니다!

\[F = \frac{SSR/p}{SST/(n-p-1)} = \frac{R^2/p}{(1-R^2)/(n-p-1)} \quad \sim F_{(p, n-p-1)}\]

R 실습 및 해석

자, 여기까지 선형 회귀와 관련하여 알아야 할 개념들을 모두 훑었습니다! 그러면 직접 선형 회귀를 적합시켜서 output을 해석해보겠습니다. 일단 먼저 R로 해보겠습니다. 데이터는 아주 유명한 보스턴 집값 데이터로 하겠습니다:) 데이터 설명은 생략하도록 하겠습니다.

library(MASS)
data(Boston) #boston data load

Boston$chas <- factor(Boston$chas) #factorize

fit <- lm(medv ~ ., Boston)
summary(fit)

코드가 정말 간단하죠? 이제 위의 아웃풋을 보면서 결과를 해석해보겠습니다.

Coefficients 관련 통계량

각 변수들의 추정치(Estimate), 표준오차(Std.Error), t-value, P-value가 나와있네요. 다만, 여기서 추정치들의 크기가 워낙 작아서 알아보기 힘들게 나와있습니다. 그래서, 소수점 4째 자리까지 반올림을 해주었어요!

round(fit$coefficients,4)

각 회귀계수에서 빨간색으로 표시한 것은 집값과 음의 관계를 가진 변수들, 파란색으로 표시한 것은 집값과 양의 관계를 가진 변수들을 의미합니다! 범죄율(crim), 환경오염정도(nox) 거리(dis) 등은 확실히 집값과 음의 관계를 띄고 있고, 강의 존재여부(Chas), 방 개수(rm) 등은 집값과 양의 관계를 가지고 있는 것을 확인할 수 있습니다. 그리고, 이 중에서 몇개만 한번 해석을 해보겠습니다.

  • $chas1=2.6867$ : 찰스강 경계에 위치한 경우(1)는 위치하지 않는 경우(0)보다 평균 집값이 2.69(단위:$1000) 더 높다.

  • $nox = -17.7667$ 농축 일산질소가 한 단위 증가할 때 평균 집값이 17.767만큼 감소한다.

Model 관련 통계량

  • Multiple R-squared($R^2$): 0.7406

  • Adjusted R-squared($R^2_{adj}$): 0.7388

  • F-statistic: 108.1 (df1=13, df2=492)

  • p-value: <0.01

일단 $R^2$가 0.7406 정도 되는데, 엄청 높은 건 아니지만, 그래도 낮은 값은 아닌 것을 확인할 수 있습니다. F-statistic은 108.1로 이 때 p-value는 매우 작은 값입니다. 따라서, 유의수준 5% 하에서 귀무가설을 기각하여, 해당 모델은 유의하다고 결론 내릴 수 있습니다.

Python 코드

파이썬은 sklearn을 이용해서 linear regression을 적합하는 경우가 가장 유명하다고 볼 수 있는데요. 그런데, 이렇게 할 경우에는 R처럼 선형 회귀 아웃풋을 다 보여주지는 않습니다. 알아서 직접 계산해야 하죠..! 그런데, statsmodels.formula.api 패키지를 이용하면, R과 비슷하게 선형 회귀 아웃풋을 얻을 수 있습니다! 코드는 다음과 같고, 해석은 R의 결과와 같으므로 생략하도록 하겠습니다.

import numpy as np
import pandas as pd
from sklearn import datasets
from statsmodels.formula.api import ols

boston = datasets.load_boston()

X = pd.DataFrame(boston.data, columns=boston.feature_names)
y = pd.DataFrame(boston.target, columns=["MEDV"])

X['CHAS'] = X['CHAS'].astype('category')

df = X.copy()
df['MEDV'] = target

model = ols('MEDV~'+"+".join(X.columns), df).fit()
model.summary()



이번 포스트는 정말 길었던 것 같네요.. 후! 이렇게 선형 회귀를 적합시켰다고 해서 끝이 아니죠. 선형 회귀의 필수 가정들이 만족하고 있는지 파악해야 합니다. 다음 포스트에서는 회귀 진단에 대해 살펴보겠습니다! 감사합니다 :)

$Reference$

  • Regression Analysis by Example 5th edition, Samprit Chatterjee $\cdot$ Ali S. Hadi, 2015