[머신러닝의 해석] 4편. Feature의 평균 영향력 및 관계 파악: PDP plot (Partial Dependence Plot) | Python

About Interpretable Machine Learning

이번 포스트는 저번 포스트에 이어서 Model-agnostic(모델에 구애받지 않는) 방법 중 하나인 Partial Dependence Plot(PDP)에 대해서 알아보겠습니다. PDP는 관심 대상인 변수와 Target 간에 어떠한 관계가 있는지 플랏으로 나타내어 확인하는 방법입니다. 이 때, 관심 대상인 변수는 최대 2개까지 함께 확인할 수 있습니다. 아무래도, 변수가 2개를 넘게 되면, Target까지 합쳐서 축이 3개를 넘어가면서 시각적으로 표현하기 매우 어려울 것입니다. 아무튼 PDP는 매우 직관적이면서, 어느 모델이든 학습시킨 후에 적용할 수 있다는 점에서, 알아두면 좋은 방법 중 하나인 것 같습니다.

이론적 아이디어


통계학과 사람들에게는 아마도 partial이라는 단어가 친숙할 것 같습니다! 선형 회귀 배울 때, 특정 변수의 회귀 계수는 ‘partial’ 회귀 계수이고, 이에 대한 해석으로는, 다른 변수들의 영향을 모두 고정한 상황에서, 해당 변수를 한 단위(1-unit) 증가시킬 때 변화하는 y(target)의 크기로 배우곤 했었는데요. PDP도 이와 비슷한 맥락입니다. 그런데, PDP는 선형적인 관계뿐 아니라, 복잡한 관계도 나타낼 수 있다는 게 큰 차이점입니다.

이제 PDP의 이론적 아이디어를 살펴보겠습니다. 먼저 기본 확률론에 대해서 리마인드를 하자면, 두 개의 랜덤 변수 $X, Y$가 존재할 때, 두 변수의 결합 분포(joint distribution)를 $Y$에 대해 기대값을 취하면, $X$의 주변 분포(marginal distribution)를 얻게 됩니다.

\[f_X(x) = \mathbb{E}_Y [ f_{X,Y} (x,y)] = \int_Y f_{X,Y}(x,y) f_Y(y) \space dy\]

PDP에서는 이를 이용합니다. 관심 있는 변수들을 $X_S$, 그 외의 변수들을 $X_C$라고 할 때, $X_S$의 Partial Dependence Function은 다음과 같이 계산됩니다.

\[f_{X_S}(x_s) = \mathbb{E}_{X_C} [f_{X_S,X_C} (x_s, x_c)] = \int f_{X_S,X_C} (x_s, x_c)f_{X_C}(x_c)\space dx_c\]

즉, 관심 대상이 아닌 변수들의 분포에 대해 주변화하는 작업을 통해, 관심 대상인 변수에만 의존하는 함수를 구하는 것입니다. 이 함수는, 관심 대상인 변수의 각 값에 대해, 평균 Marginal Effect가 어느정도 되는지를 나타내는 것으로 해석할 수 있습니다. 그런데, 위의 공식과 같이 주변 분포를 구하기 위해서는, 결합 분포, 관심 대상이 아닌 변수들의 주변 분포를 알아야 하는데, 실제 그 분포를 아는 경우는 거의 없을 것입니다. 그렇다면, 이 아이디어를 실제로 어떻게 구현을 하는 걸까요?


실제로 구현되는 아이디어


분포를 몰라서 $X_S$의 Partial Dependence Function을 구할 수 없다면, 주어진 데이터를 가지고 이에 근사하는 함수를 추정해야 할 것입니다. 추정하는 아이디어는 정말 간단합니다. 먼저, 전체 샘플의 개수가 $n$개라고 할 때, 근사 함수는 다음과 같이 계산됩니다.

\[f_{X_S}(x_s) \approx \hat f_{X_S}(X_S) =\frac{1}{n}\sum^n_{i=1} f(x_S, x_c^{(i)})\]

$x_c^{(i)}$는 $X_C$ 변수의 i번째 샘플값을 의미합니다. 즉, 고정된 $x_s$값에 대한 $X_S$의 Partial Dependence Function의 함숫값으로, $X_S$ 변수의 모든 샘플값을 $x_s$으로 고정했을 때의 전체 예측값들을 평균값을 추정하는 것입니다. 대체 뭔 소린지 모르시겠다구요? 정말 쉽게 풀어서 설명해보겠습니다!

구현 아이디어

  • (1) 데이터에 등장하는 $X_S$(관심 변수)의 모든 값에 대해 하나씩, 해당 변수의 모든 샘플을 그 값으로 대체한 후 이미 학습시킨 모델을 통해 각 샘플에 대한 예측값을 구한다. 예를 들어, 성별이 관심 변수일 때, 해당 변수의 모든 값을 ‘여성’으로 대체한 후 예측값을 구하고, 그 뒤에는 모든 값을 ‘남성’으로 대체한 후 예측값을 구한다.

  • (2) 관심 변수의 각 값에 대해, 구한 예측값들을 평균 낸다. 각 값에 따라, 평균 예측값이 어떻게 변화하는지 플랏으로 나타낸다. 즉, x축은 [여성, 남성]일 것이고, y축에 해당하는 값은 각각 [여성일 때 예측값의 평균, 남성일 때 예측값의 평균]일 것입니다.

정말 직관적이고 간단하지 않나요? 이렇게 전체 샘플의 값을 평균내어 평균적인 Marginal Effect를 확인한다는 점에서, PDP는 Global한 방법입니다. (Global의 의미에 대해서는 이곳을 참고해주세요.)


주의할 점


그런데 PDP 사용하기 전, 유의해야 할 몇가지 상황들이 있습니다.

  • 샘플 수가 굉장히 많거나 관심 변수의 cardinality가 매우 클 경우
    구현 아이디어를 보고 느낌이 오신 분들도 많겠지만, 이 방법은 데이터가 크거나, 변수의 값이 매우 많은 연속형 변수일수록 연산량이 방대해집니다. 변수의 Parameter Space를 구성하는 원소들, 즉 해당 변수에 등장하는 값들이 정말 다양할 경우, 반복 횟수가 늘어나기 때문이죠. 뒤에 예시에서 보겠지만, 제가 실제로 적용해보았을 때에도, 범주형 변수는 굉장히 빨리 아웃풋이 나왔지만, 연속형 변수는 시간이 오래 걸렸습니다. 따라서, 웬만하면, cardinality가 비교적 작은 변수이거나 중요한 변수 한,두가지만 PDP를 통해 살펴보는 것이 좋을 것 같습니다.

  • 변수 간 상관성이 매우 클 경우
    한편, PDP에서는 각 변수들이 서로 상관관계가 없다고 가정합니다. 관심 대상인 변수들과 관심 대상이 아닌 변수들 간 상관관계가 없다고 가정하여, 관심 대상인 변수와 Target 간의 순수한 관계를 보겠다는 의미인데요. 사실상 실제로 각 변수들 간 서로 영향이 전혀 없는 데이터가 몇이나 될까요? 대부분, 이 가정을 정확히 지키면서 사용하지는 않는 것 같습니다..! 다만, 상관성이 너무 높은 변수들이 있다면, PDP를 적용하기 전 유의해야 합니다. 매우 비현실적인, 분포적으로 등장할 확률이 매우 적은 샘플 경우들이 생성되어, 전체 예측값 평균 계산에 영향을 끼칠 수 있기 때문입니다.

  • 샘플 간 성질이 매우 다를 경우
    대부분의 Global Method들의 한계라고 할 수 있을 것 같은데, 샘플들의 성질이 매우 다를 경우에는 참고할 만한 좋은 플랏이 되지 못합니다. 예측값들을 평균낸 값들로 영향을 보는 것이기 때문에, 샘플들의 서로 다른 성질들이 반영되지 못합니다. 예를 들어, 절반은 예측값이 100이고, 절반은 예측값이 -100일 때, 평균은 0이 될 것입니다.


적용하기


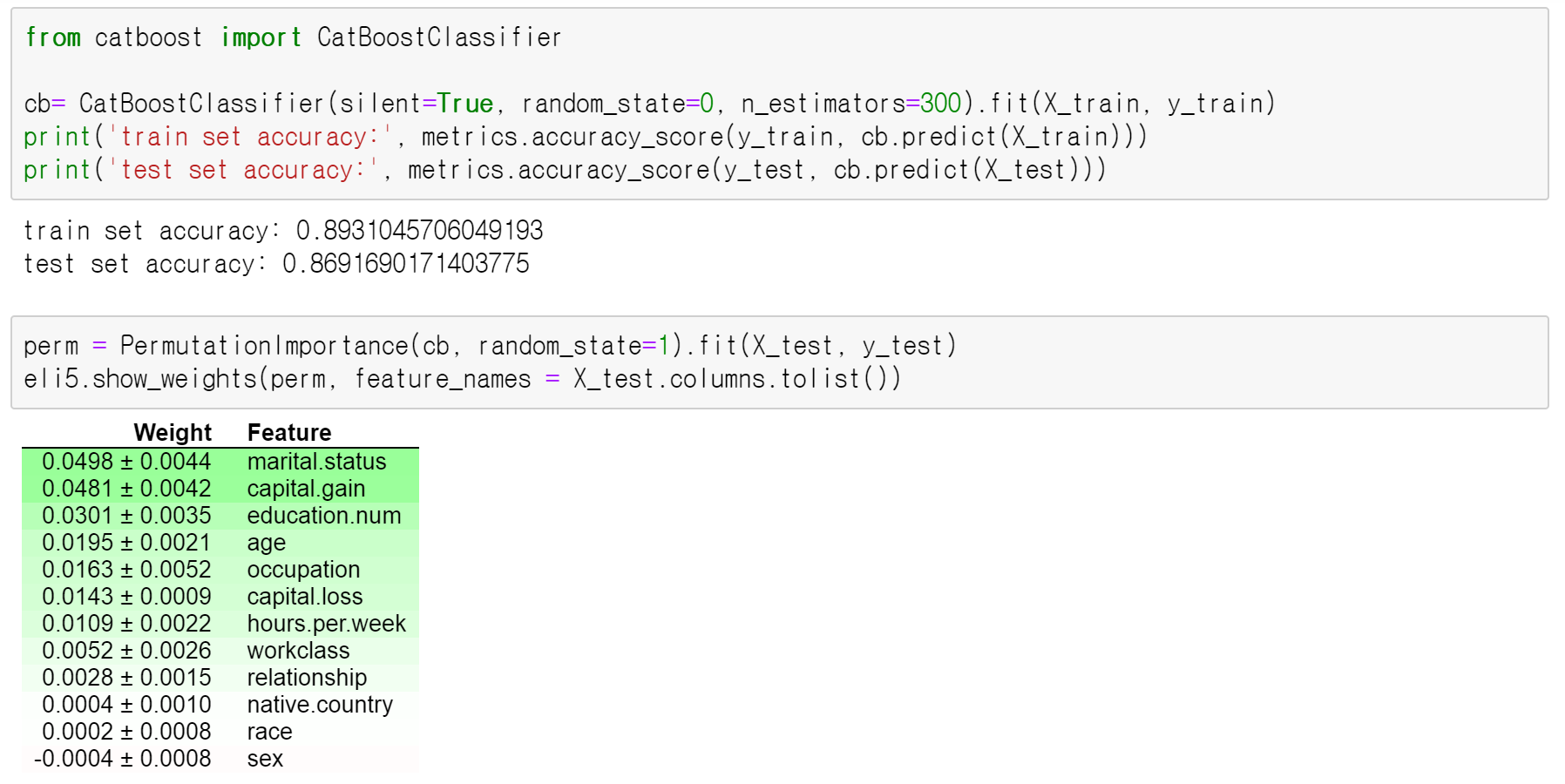
이제 sklearn을 이용해서 PDP를 적용해보겠습니다! 이번에도 마찬가지로 머신러닝의 해석 시리즈에서 쭉 사용되고 있는 데이터를 이용합니다.(데이터 설명은 이곳을 참고해주세요.) 저번 포스트에서 Catboost 분류기를 이용해서 학습을 시키고, Permutation Feature importance로 변수 중요도를 파악한 결과, marital.status, capital.gain, education.num의 세 변수가 가장 중요하게 나왔는데요. 아래 내용에 대한 코드는 이곳에 있습니다.

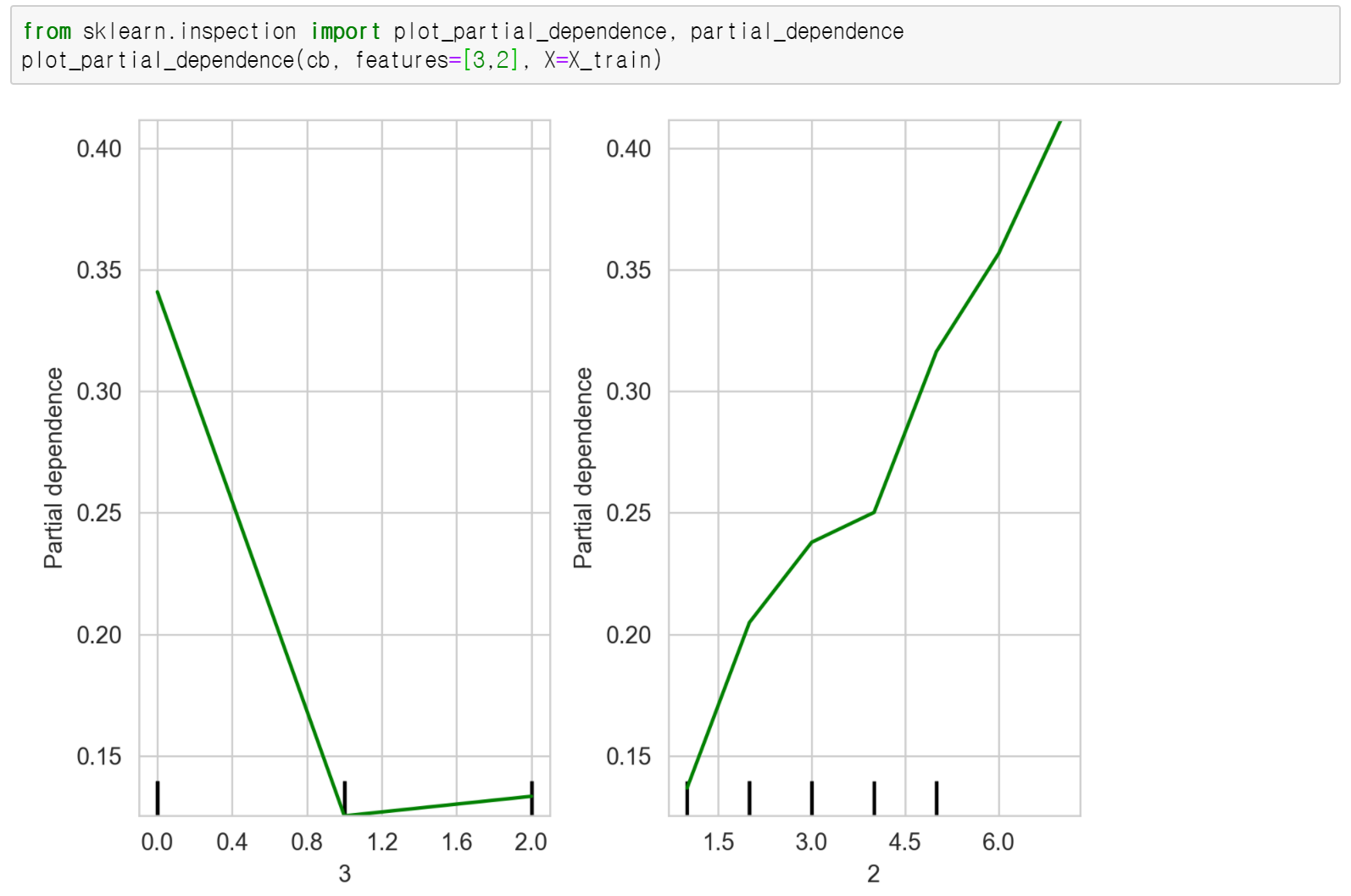
먼저, 이 세 변수 중 범주형에 해당하는 두 변수 marital.status, education.num에 대해, PDP를 구해보았습니다. 학습한 모델, 해당 변수들의 칼럼 위치, 데이터를 차례로 집어넣기만 하면, 다음의 플랏이 나오는데요. 이 상태에서는, x축 레이블이나 색깔 등 맘대로 변경하기가 어려워서 값만 얻어서 새로 플랏을 그려보기로 했습니다.

(1) marital.status

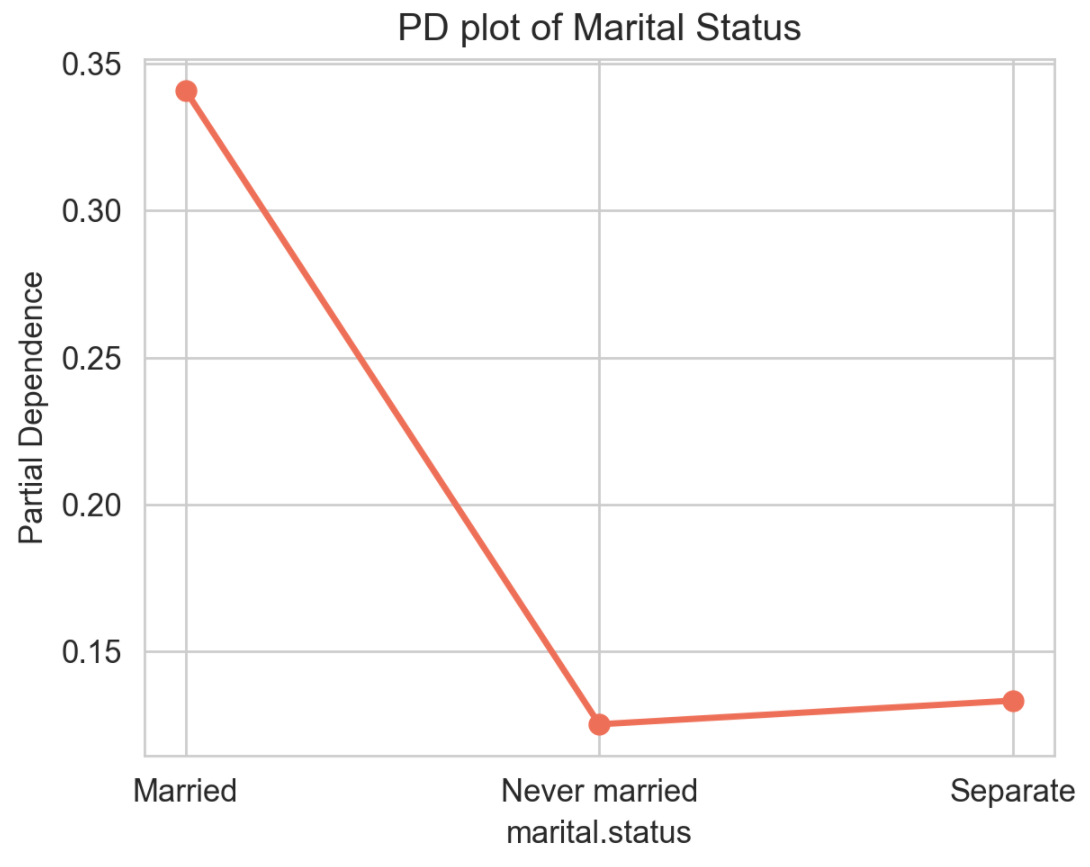
먼저, 변수 marital.status의 경우, 카테고리가 3개(‘Married’, ‘Never Married’, ‘Separate’)였고, Partial dependence의 값과 x축의 값을 뽑아보면 다음과 같습니다.

이제 이 값들을 이용해서, 좀 더 깔끔하게 플랏으로 나타내보면 다음과 같습니다! 결혼을 하고 현재도 같이 살고 있을수록(Married), 1(연봉이 $50,000이상)로 분류될 확률이 가장 높은걸 볼 수 있습니다!

나머지 변수들도 나타내보면 다음과 같습니다.

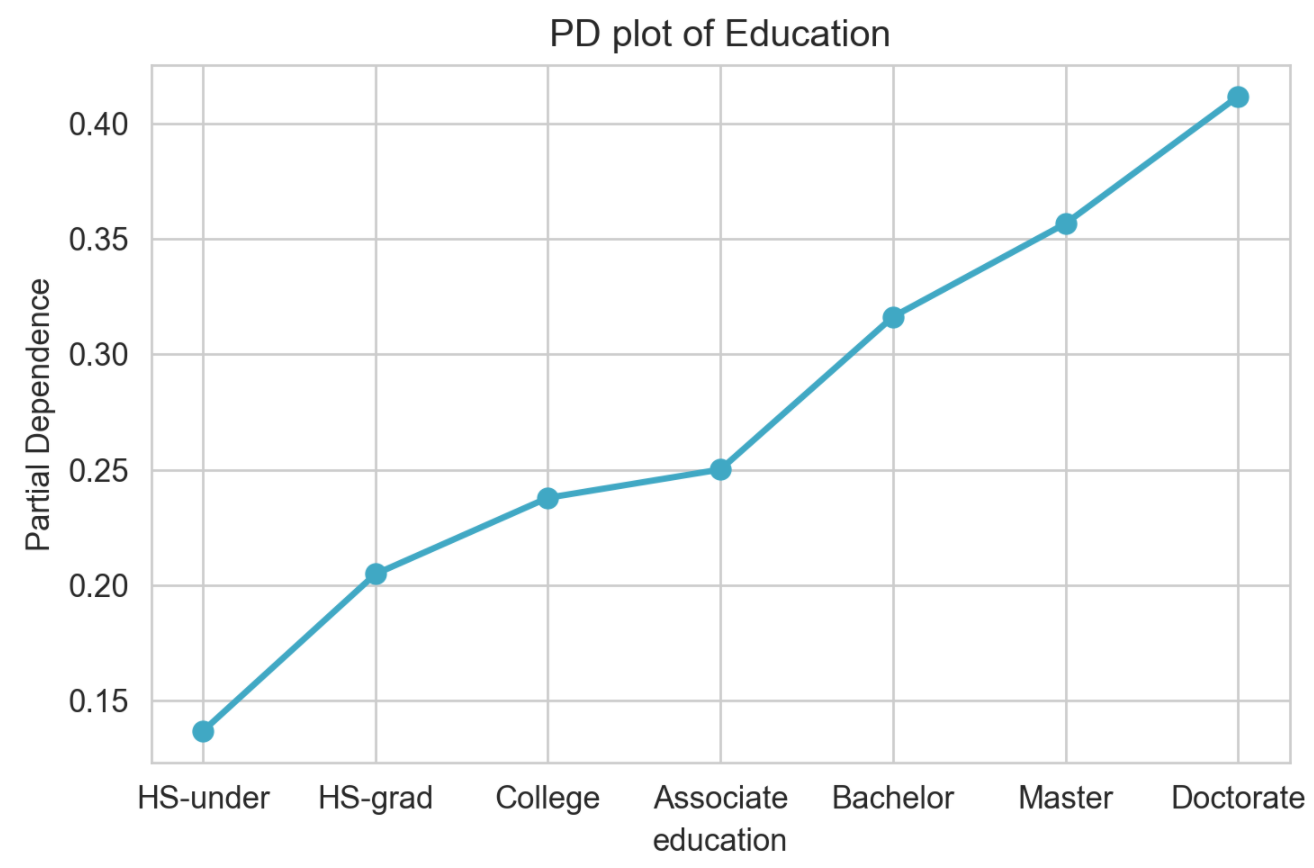
(2) education.num

확실히 교육 수준이 높아질수록, 1로 분류될 확률이 높은 걸 확인할 수 있습니다.

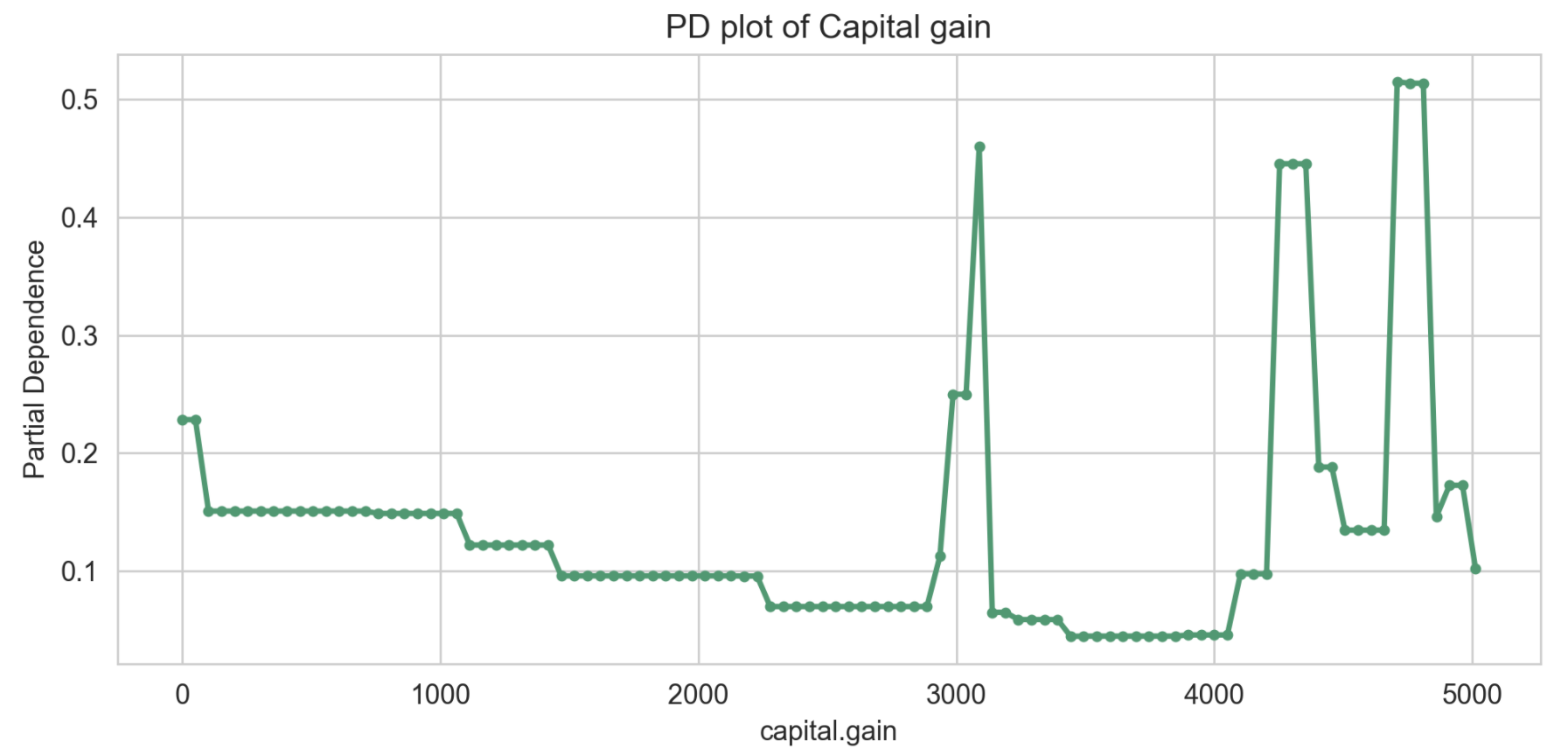
(3) capital.gain

한편, capital.gain의 경우, 3000에서 한번 치솟고, 그 뒤에 4000 이상부터 1로 분류될 확률이 높아집니다. 연속형 변수이기 때문에, PDP를 구하는데 시간이 위 두 변수들에 비해 오래 걸렸습니다.


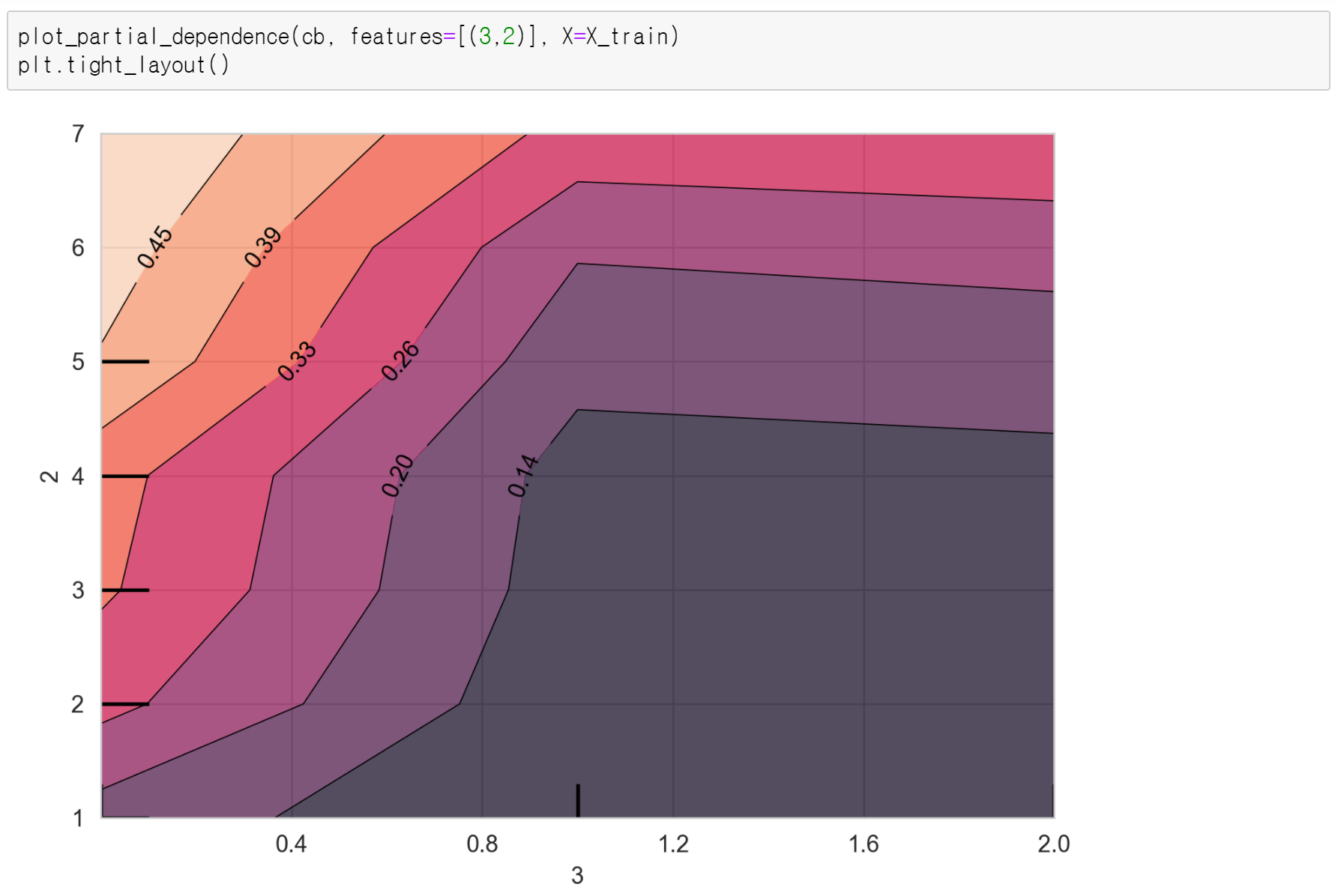
이렇게 중요하게 뽑힌 변수들 각각에 대해, Target과 어떤 영향이 있는지 파악해 보았습니다. 한편, 관심 변수는 꼭 하나 말고 2개까지도 가능합니다! marital.status와 education.num의 Two-way PDP를 한번 그려보면 다음과 같습니다. x축이 marital.status, y축이 education.num인데, 교육수준이 높고 배우자와 함께 살고 있는 사람일수록 연봉이 $50,000이상일 확률이 높습니다. 그런데 이 확률 값이, 두 변수 개별 플랏에서 확인했던 최대치보다 높습니다! 즉, 두 변수가 모이니까 1로 분류될 확률이 더 높아졌네요.


여기까지 PDP에 대해서 살펴보았습니다! 다음 포스트에는 앞부분은 PDP와 똑같지만 global 방법이 아닌, Independent Conditional Expectation(ICE)에 대해서 살펴보겠습니다.


$Reference$